里面是一些杂七杂八的数学知识,不定期更新(雾)。
Circulant Matrix
An circulant matrix takes the form
It has the determinant , where and .
ProofLet , then
Therefore , .
Gridiant of Log-Determinant Function
Let be a positive definite matrix, then .
ProofLet , then
where are the eigenvalues of . Since , we have , and thus . Therefore
Thus, .
Barbalat’s Lemma
If is uniformly continuous with , then .
For series we have . However, for functions , the uniform continuity is necessary.
- Example 1.
Since , by Dirichlet’s test, the integral converges. However, does not exist.- Example 2.
Define and , then is monotonic increasing on and . We have Here we use the inequality and the fact that . Therefore, exists. By increasing, , but doesn’t exist.
ProofIf as , then there exists and a sequence such that . Since is uniformly continuous, . So , we have . Therefore
However, since exists. LHS converges to 0 as , yielding a contradiction.
Perron-Frobenius Theorem
DefinitionPositive Matrix
A positive(non-negative) matrix is a matrix with all entries positive(non-negative). If , then .
DefinitionSpectral Radius
The spectral radius of a matrix is defined as .
Let be a positive matrix, then
- has a positive eigenvalue with respect to a positive eigenvector (Perron–Frobenius eigenvalue).
- Perron–Frobenius eigenvalue is simple (i.e. the algebraic multiplicity of is both 1).
- There are no other positive eigenvectors except positive multiples of .
LemmaGelfand’s formula
If and , then with the spectral norm.
ProofWe can suppose that
Let be an eigenvalue of with and the corresponding eigenvector. Consider , then we have
which implies . Now we prove that is impossible. Suppose that , then
Thus, , and by induction we have , which implies . Therefore
which contradicts Gelfand’s formula. Therefore, which means there exists a positive eigenvector with respect to eigenvalue .
Assume that there exists an eigenvector that is linearly independent with and corresponds to the eigenvalue . Let (if , we can choose ), then we have and . However, since , , which contradicts the fact that . Therefore, the geometric multiplicity of is 1.
Using the fact that is also positive, there exists a positive eigenvector with respect to the eigenvalue . Note , we have . Since , then . Choose a basis for , then the matrix of under is
If there exists a positive eigenvector of with respect to the eigenvalue , then , which implies and are linearly dependent, contracting the fact that the geometric multiplicity is 1. Therefore, the algebraic multiplicity of is also 1.
Suppose there exists a positive eigenvector corresponding to the eigenvalue , then by the positivity of , . Let , then . However, since , , which means , yielding a contradiction. Therefore, there are no other positive eigenvectors except positive multiples of .
KL Divergence
DefinitionIf and are two probability distributions, then the Kullback-Leibler divergence from to is defined as
Positivity
ProofHere we use the Jensen’s inequality since is a convex function.
Forward and Reverse KL Divergence
If we use the dstribution to approximate the distribution , then
Minimizing forwad KL divergence is equivalent to make a maximum likelihood estimation of under .
ProofHere we use to represent the data we collected.
Wherever has high probability, must also have high probability.
The figure above shows the effect of fitting a bimodal distribution using a unimodal distribution through the forward KL divergence cost.
This property of the forward KL divergence is also often referred to as “zero avoiding”, because it tends to avoid having at any position where .
Minimizing reverse KL divergence is equivalent to requiring that the fitting maintains a single mode as much as possible.
ProofBased on the properties of entropy, it is known that when approaches a uniform distribution, the value of is larger. Conversely, when tends toward a unimodal distribution (single-peak distribution), the value of is smaller. Therefore, the reverse KL divergence is equivalent to requiring to fit while maintaining as much unimodality as possible.
Wherever has high probability, must also have high probability.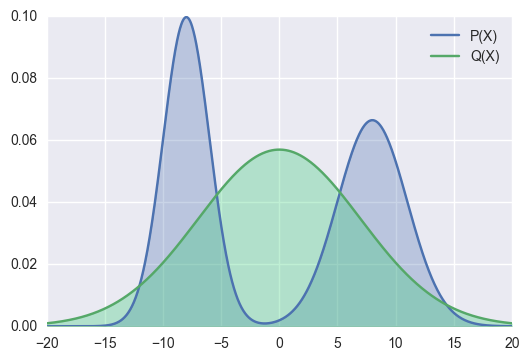
The figure above shows the effect of fitting the same bimodal distribution using a unimodal distribution through the reverse KL divergence cost.
The reverse KL divergence tends to minimize the difference between and when .
