本篇是 Adam B Kashlak 老师的 Probability and Measure Theory 课程笔记

Measure Theory#

Measures and $\sigma$ -Fields#

$\sigma$ -Field #

Question : What sets (subsets of $\Omega$ ) am I allowed to measure?

Definition
For some set $\Omega$ , a $\sigma$ -Field $\mathcal{F}$ is a collection of sets $A\in \Omega$ s.t.
$\varnothing, ~\Omega \in \mathcal{F}$
If $A\in \mathcal{F}$ then $A^c \in \mathcal{F}$
$\mathcal{F}$ is closed under union: for a countable collection of sets $\{A_i\}_{i=1}^\infty$ s.t. $A_i \in \mathcal{F}$ for all $i\in \mathbb{N}$ then $\bigcup_{i=1}^{\infty} A_i \in \mathcal{F}$
Equivalence : $\mathcal{F}$ also contains countable intersections because $~\bigcap_{i=1}^{\infty} A_i = \bigcup_{i=1}^{\infty} A_i^c\in \mathcal{F}$

Measure#

Definition
A measure $\mu~:~\mathcal{F}\rightarrow\mathbb{R}_+$ is a mapping from a $\sigma$ -field $\mathcal{F}$ to the non-negative real numbers s.t.
$\mu(\varnothing) = 0$
For a pairwise disjoint collection $\{A_i\}_{i=1}^\infty$ then $\mu\left(\bigcup_{i=1}^{\infty} A_i\right) = \sum_{i=1}^{\infty} \mu(A_i)$ (Countably Additivity)

Special Cases for a Measure Space $(\Omega, \mathcal{F}, \mu)$ :

If $\mu(\Omega) = 1$ then we say that $(\Omega, \mathcal{F}, \mu)$ is a Probability Measure
If $\mu(A) < \infty$ for any $A$ then we say that $\mu$ is a Finite Measure
If $\Omega=\bigcup_{i=1}^{\infty} A_i$ s.t. $\mu(A_i) < \infty ~~ \forall i~$ then $\mu$ is a $\sigma$ -Finite Measure
Example
$\Omega=\mathbb{R}~$ , $\mu([a,b])=b-a$ and $\mathbb{R}= \bigcup_{i=1}^{\infty} [i-1,i]\cup[-i,-i+1]$ then $\mu$ is a $\sigma$ -Finite Measure

Power Set#

Definition
Power set $\mathscr{P}(\Omega)$ or $2^\Omega$ is the set of all subsets of $\Omega$

Semi-Ring of Sets#

Definition
$\mathcal{A}$ , a collection of subsets of $\Omega~$ , is called a Semi-Ring when
$\varnothing \in \mathcal{A}$
If $A, B \in \mathcal{A}$ then $A\cap B \in \mathcal{A}$
If $A, B \in \mathcal{A}$ then there exists a finite number of pariwise disjoint sets $C_i \in \mathcal{A}$ for $~i=1,\cdots,n~$ s.t. $A\setminus B = \bigcup_{i=1}^{n} C_i$

Example
$\mathcal{A}$ : all intervals $(a,b]$ in $\mathbb{R}$ is a semi-ring

Ring of Sets#

Definition
$\mathcal{A}$ , a collection of subsets of $\Omega~$ , is called a Ring when
$\varnothing \in \mathcal{A}$
If $A, B \in \mathcal{A}$ then $A\setminus B \in \mathcal{A}$
If $A, B \in \mathcal{A}$ then $A\cup B\in \mathcal{A}~$ (This implies finite unions are also in $\mathcal{A}$ )

From the defintion, we know that the intersection of two sets is also in $\mathcal{A}$ because $A\cap B = A\setminus (A\setminus B)$

Example
All finite unions of half open intervals $(a,b]$ in $\mathbb{R}$ is a ring

Field#

Definition
$\mathcal{A}$ is a Field if it is a Ring and $\Omega \in \mathcal{A}$

Equivalence
Since the whole set $\Omega$ is in $\mathcal{A}$ , then
the second condition of Ring is equivalent to $\mathcal{A}$ being closed under complimentation as $A \setminus B = A \cap A^c$ and $A^c = \Omega \setminus A$
the third condition of Ring is equivalent to $\mathcal{A}$ being closed under finite unions as $A\cup B = (A^c \cap B^c)^c$

Note : Field + countable unions $=$ $\sigma$ -Field

Set Function#

Definition
A set function $\mu: ~\mathcal{A}\rightarrow \mathbb{R}^+$ (not necessarily a measure) is a mapping from a set of functions $\mathcal{A}$ to $\mathbb{R}^+$ . For $A, B \in \mathcal{A}$ , we say that
$\mu$ is monotone if $A\subset B$ implies $\mu(A)\leq \mu(B)$
$\mu$ is additive if $\mu(A\cup B) = \mu(A) + \mu(B)$ for $A, B$ disjoint
$\mu$ is countably additive if $\mu\left(\bigcup_{i=1}^{\infty} A_i\right) = \sum_{i=1}^{\infty} \mu(A_i)$ for $\{A_i\}_{i=1}^\infty$ pairwise disjoint and $\bigcup_{i=1}^{\infty} A_i \in \mathcal{A}$
$\mu$ is countably sub-additive if $\mu\left(\bigcup_{i=1}^{\infty} A_i\right) \leq \sum_{i=1}^{\infty} \mu(A_i)$ for $\bigcup_{i=1}^{\infty} A_i \in \mathcal{A}$ (not nessarily pairwise disjoint)
$\mu$ is a pre-measure if $\mu$ is countably additive, $\mu(\varnothing)=0$ and $\mathcal{A}$ is a ring. For a pre-measure, it is also
monotone because for $A\subset B$ we have $\mu(B)=\mu(A\cup (B\setminus A)) = \mu(A) + \mu(B\setminus A) \geq \mu(A)$
sub-additive because for $\bigcup_{i=1}^{\infty} A_i \in \mathcal{A}$ let $B_i=A_i \setminus \left(\bigcup_{j=1}^{i-1} A_j\right)$ then $B_i$ are pairwise disjoint and by monotonicity, $\mu\left(\bigcup_{i=1}^{\infty} A_i\right) = \mu\left(\bigcup_{i=1}^{\infty} B_i\right) = \sum_{i=1}^{\infty} \mu(B_i) \leq \sum_{i=1}^{\infty} \mu(A_i)$

Outter Measure#

Definition
For a pre-measure $\mu$ on a ring $\mathcal{A}$ , the outter measure (Not necessarily a Measure) $\mu^* : \mathcal{M} \rightarrow \mathbb{R}^+$ is defined as
$\mu^*(E) = \inf \left\{ \sum_{i=1}^{\infty} \mu(A_i) ~:~ E\subset \bigcup_{i=1}^{\infty} A_i, ~A_i\in \mathcal{A} \right\}$
for any $E\subseteq \Omega$ . This is equal to the smallest possible sum of the pre-measure over all finite or countable collections of $A_i$ in $\mathcal{A}$ that cover $E$ .

Can we “Measure” (Outer Measure) any $E\subset \Omega$ ? Not necessarily

Denote $\mathcal{M}$ to be the collection of all $\mu^*$ measurable sets where we say that $B\subseteq \Omega$ is $\mu^*$ measureable when

\mu^*(E\cap B) + \mu^*(E\cap B^c) = \mu^*(E) ~~ \forall E\subseteq \Omega

Caratheodory Extension Theorem#

Caratheodory Extension Theorem
Let $\mathcal{A}$ be a ring on $\Omega$ and $\mu$ be a pre-measure, then $\mu$ extends to a measure on $\sigma(\mathcal{A})$ .

Note
$\sigma(\mathcal{A})$ is the $\sigma$ -field comes from extend $\mathcal{A}$ by including coutable unions and $\Omega$ itself.
The “corret” extension is the outter measure $\mu^*$ .

Proof
Assume $B\subset \Omega$ and $\mu^*(B)<\infty$
Prove stuff about $\mu^*$
$\mu^*(\varnothing)=0$ as $\mu$ is a pre-measure
$\mu^*$ is non-negative as $\mu$ is non-negative
$\mu^*$ is monotone (increasing)
Let $B_1, B_2 \subset \Omega$ and $B_1\subset B_2$ then for any ${A_i}$ s.t. $B_2 \subseteq \bigcup_i A_i$ . Then $B_1 \subseteq \bigcup_i A_i$ thus $\mu^*(B_1)\leq \mu^*(B_2)$
$\mu^*$ is countably sub-additive
For $\{B_i\}_{i=1}^\infty$ and a given $\epsilon > 0$ , let $B_i\subseteq \bigcup_i A_{ij}$ for $A_{ij}\in \mathcal{A}$ s.t.
$\sum_i \mu(A_{ij}) \leq \mu^*(B_i) + \epsilon\cdot 2^{-i}$
This is possible because $\mu^*$ is the infimum. As $\bigcup_{i=1}^\infty B_i \subseteq \bigcup_{i,j} A_{ij}$ and as $\mu^*$ is monotone and $\mu$ is sub-additive, then
$\begin{aligned} \mu^*\left(\bigcup_{i=1}^\infty B_i\right) &\leq \mu\left(\bigcup_{i,j} A_{ij}\right) \\ &\leq \sum_{i,j} \mu(A_{ij}) \\ &\leq \sum_i \mu^*(B_i) + \epsilon\cdot 2^{-i} \end{aligned}$
Take $\epsilon\rightarrow 0$ to get that $\mu^*$ is countably sub-additive
Check that $\mu$ and $\mu^*$ coincide for all $A\in \mathcal{A}$
For any $A\in \mathcal{A}$ we have $\mu^*(A) \leq \mu(A)$ because $\{A\}$ is a cover of $A$ and $\mu^*$ is the infimum
For the reverse, if $A\subset \bigcup_i A_i$ then by countable sub-additivity and monotonicity
$\mu(A) \leq \sum_i \mu(A\cap A_i) \leq \sum_i \mu(A_i)$ This implies that $\mu(A)\leq \mu^*(A)$ because the right hand side is the cover of A.
Thus $\mu(A)=\mu^*(A) ~~ \forall A\in \mathcal{A}$
Check that the ring $\mathcal{A}\subset \mathcal{M}$ (all $\mu^*$ measurable sets)
i.e. $\forall A \in \mathcal{A}$ we want to show that $A$ is $\mu^*$ -measurable: $\mu^*(E\cap A) + \mu^*(E\cap A^c) = \mu^*(E) ~~ \forall E\subseteq \Omega$
Note $\mu^*(E \cap A) + \mu^*(E\cap A^c) \geq \mu^*(E)$ as $\mu^*$ is sub-additive.
Next, for some $\epsilon>0~$ , choose $\{A_i\}$ s.t. $E\subset \bigcup_i A_i$ and $\sum_i \mu(A_i) \leq \mu^*(E) + \epsilon$
Furthermore, $E\cap A\subset \bigcup_i(A\cap A_i)$ and $E\cap A^c \subset \bigcup_i(A^c\cap A_i)$ thus $\begin{aligned} \mu^*(E\cap A) + \mu^*(E\cap A^c) &\leq \sum_i \mu(A\cap A_i) + \sum_i \mu(A^c\cap A_i) \\ &= \sum_i \mu(A_i) \leq \mu^*(E) + \epsilon \end{aligned}$ and take $\epsilon\rightarrow 0$ .
Show that $\mathcal{M}$ is a $\sigma$ -Field
$\varnothing \in \mathcal{M}$ since $\varnothing \in \mathcal{A}$
$\Omega \in \mathcal{M}$ since $\forall E\subset \Omega ~~ \mu^*(E\cap \Omega) + \mu^*(E\cap\varnothing)=\mu^*(E)$
$\mathcal{M}$ is closed under coplimentation since $\mu^*(E\cap B^c) + \mu^*(E\cap (B^c)^c) = \mu^*(E)$ which implies that $B^c \in \mathcal{M}$
$\mathcal{M}$ is closed under finite intersections since for $B_1, B_2\in\mathcal{M}$ and any $E \subset \Omega$ $\begin{aligned} \mu^*(E)&=\mu^*(E\cap B_1) + \mu^*(E\cap B_1^c) \\ &= \mu^*(E\cap B_1\cap B_2) + \mu^*(E\cap B_1^c\cap B_2) + \mu^*(E\cap B_1\cap B_2^c) + \mu^*(E\cap B_1^c\cap B_2^c) \\ &\geq \mu^*(E\cap B_1\cap B_2) + \mu^*(\{E\cap B_1^c\cap B_2\}\cup\{E\cap B_1\cap B_2^c\}\cup \{E\cap B_1^c\cap B_2^c\}) \\ &=\mu^*(E\cap \{B_1\cap B_2\}) + \mu^*(E\cap \{B_1\cap B_2\}^c) \geq \mu^*(E) ~~~~~(\text{sub-additivity}) \end{aligned}$ thus $B_1\cap B_2 \in \mathcal{M}$ . Properties above show that $\mathcal{M}$ is a Field.
To get to a $\sigma$ -Field, let $\{B_i\}$ in $\mathcal{M}$ be countable and parwise disjoint and $\bigcup_i B_i \in \mathcal{M}$ . Let $B = \bigcup_{i=1}^\infty B_i$ , then $\begin{aligned} \mu^*(E) &= \mu^*(E\cap B_1) + \mu^*(E\cap B_1^c) \\ &= \mu^*(E\cap B_1) + \mu^*(E\cap B_2) + \mu^*(E\cap B_1^c\cap B_2^c) \\ &~~\vdots \\ &= \sum_{i=1}^n \mu^*(E\cap B_i) + \mu^*\left(E\cap\bigg\{\bigcap_{i=1}^n B_i^c\bigg\}\right) \\ \end{aligned}$ Then by monotonicity and sub-additivity and let $n\rightarrow \infty$ , we get $\begin{aligned} \mu^*(E) &= \sum_{i=1}^{\infty} \mu^*(E\cap B_i) + \mu^*(E\cap B^c) \\ &\geq \mu^*(E\cap B) + \mu^*(E\cap B^c) \\ &\geq \mu^*(E) \end{aligned}$ Thus $\mathcal{M}$ is closed under countable unions ( $\mathcal{M}$ is a $\sigma$ -Field！). Choose $E = B$ we have $\mu^*(E)=\sum_{i=1}^\infty \mu^*(E\cap B_i)$ which means $\mu^*$ is countably additive.
Conclusion: $\mu^*$ is a set function $2^\Omega\rightarrow \mathbb{R}^+$ and it’s also a measure on $\mathcal{M}$ . Since $\mathcal{A}\subset \mathcal{M}$ , then $\sigma(\mathcal{A})\subseteq \mathcal{M}$ . Lastly, as $\mu^*$ is a measure on $\mathcal{M}$ , it is also a measure on $\sigma(\mathcal{A})$ . $\square$

$\pi$ -System and $\lambda$ -System #

$\pi$ -system
A collection of sets $\mathcal{A}$ is a $\pi$ -system if
$\varnothing \in \mathcal{A}$
$\forall A, B \in \mathcal{A}$ , $A\cap B \in \mathcal{A}$ .

$\lambda$ -system
A collection of sets $\mathcal{L}$ is a $\lambda$ -system if
$\Omega \in \mathcal{L}$
If $A, B \in \mathcal{L}$ and $A\subset B$ then $B\setminus A \in \mathcal{L}$ .
If $\{A_i\}_{i=1}^\infty$ is a sequence of pairwise disjoint sets in $\mathcal{L}$ then $\bigcup_{i=1}^\infty A_i \in \mathcal{L}$ .

Note : a Field is a $\pi$ -system

Example
Let $\Omega=\{1,2,3,4\}$ and $\mathcal{L}$ contains all subsets with an even number of elements. Then $\mathcal{L}$ is a $\lambda$ -system but not a $\sigma$ -Field since $\{1,2\}, \{2,3\}\in \mathcal{L}$ but $\{1,2\}\cup\{2,3\}=\{1,2,3\}\notin \mathcal{L}$

Dynkin $\pi$ - $\lambda$ Theorem #

Dynkin $\pi$ - $\lambda$ Theorem
Let $\mathcal{A}$ be a $\pi$ -system, $\mathcal{L}$ be a $\lambda$ -system and $\mathcal{A}\subseteq \mathcal{L}$ . Then $\sigma(\mathcal{A})\subseteq \mathcal{L}$ .

Proof
Let $\mathcal{L}_0$ be the smallest $\lambda$ -system such that $\mathcal{A}\subset\mathcal{L}_0$ , then $\mathcal{L}_0\subseteq\mathcal{L}$ . Our goal is to show that $\mathcal{L}_0$ is also a $\pi$ -system and a collection of sets that is both a $\pi$ -system and a $\lambda$ -system is a $\sigma$ -Field. Then we necessarily have that $\sigma(\mathcal{A})\subseteq\mathcal{L}_0\subseteq\mathcal{L}$ .
We only need to show that $\mathcal{L}_0$ is closed under intersections.
Let $\mathcal{L}'=\{B\in\mathcal{L}_0 : B\cap A\in\mathcal{L}_0, \forall A\in\mathcal{A}\}$ then $\mathcal{A}\subset\mathcal{L}'$ as $\mathcal{A}$ is a $\pi$ -system and let’s show that $\mathcal{L}'$ is also a $\lambda$ -system:
$\Omega\in\mathcal{L}'$ as $\mathcal{A}\subset\mathcal{L}_0$
If $B_1, B_2\in\mathcal{L}'$ s.t. $B_1\subset B_2$ then for any $A\in\mathcal{A}$ we have that $B_1\cap A, B_2\cap A\in\mathcal{L}_0$ . Thus $(B_2\cap A)\setminus (B_1\cap A) = (B_2\setminus B_1)\cap A\in\mathcal{L}_0$ , which implies that $B_2\setminus B_1\in\mathcal{L}'$
If $\{B_i\}_{i=1}^\infty\in\mathcal{L}'$ are pariwise disjoint, then for any $A\in\mathcal{A}$ , $A\cap B_i\in\mathcal{L}_0$ thus $\bigcup_{i=1}^\infty (A\cap B_i)\in\mathcal{L}_0$ . This implies that $A\cap(\bigcup_{i=1}^\infty B_i)=\bigcup_{i=1}^\infty (A\cap B_i)\in\mathcal{L}_0$ . Hence, $\bigcup_{i=1}^\infty B_i\in\mathcal{L}'$ .
By definition of $\mathcal{L}'$ , $\mathcal{L}'\subseteq \mathcal{L}_0$ but $\mathcal{L}_0$ is the smallest. Thus $\mathcal{L}'=\mathcal{L}_0$ and $\mathcal{L}_0$ is a $\lambda$ -system. Therefore, $\mathcal{L}_0$ contains all intersections with elements of $\mathcal{A}$ .
Lastly, let $\mathcal{L}''=\{B\in\mathcal{L}_0 : B\cap C\in\mathcal{L}_0 ~\forall~ C\in\mathcal{L}_0\}$ since $\mathcal{L}_0=\mathcal{L}'$ , $\mathcal{A}\subset \mathcal{L}''$ . Then do the same thing we did above to $\mathcal{L}''$ to show that $\mathcal{L}''$ is a $\lambda$ -system and thus $\mathcal{L}''=\mathcal{L}_0$ .
Therefore, $\mathcal{L}_0$ is closed under intersections and thus a $\sigma$ -Field. This implies that $\sigma(\mathcal{A})\subseteq\mathcal{L}_0\subseteq\mathcal{L}$ . $\square$

Uniquessness of Extension Thereom#

Uniqueness of Extension
Let $\mu_1, \mu_2$ be $\sigma$ -Finite measures on $\sigma(\mathcal{A})$ where $\mathcal{A}$ is a $\pi$ -system. Then, if $\forall A\in\mathcal{A} ~\mu_1(A)=\mu_2(A)$ then $\mu_1$ and $\mu_2$ are equal on $\sigma(\mathcal{A})$ .

Proof (Finite Measures)
Assuming $\mu_1(\Omega)=\mu_2(\Omega)<\infty$
Let $\mathcal{L}=\{B\subset\Omega : \mu_1(B)=\mu_2(B)\}$ and we only need to show that $\mathcal{L}$ is a $\lambda$ -system because since $\mathcal{A}\subset\mathcal{L}$ , by Dynkin $\pi$ - $\lambda$ Theorem, $\sigma(\mathcal{A})\subset\mathcal{L}$ which means $\mu_1=\mu_2$ coincide on $\sigma(\mathcal{A})$ .
$\Omega\in\mathcal{L}$
If $A, B\in\mathcal{L}$ with $A\subset B$ then $\begin{aligned} \mu_1(B\setminus A) + \mu_1(A)&=\mu_1(B)\\ &=\mu_2(B)\\ &=\mu_2(B\setminus A) + \mu_2(A) < \infty \end{aligned}$ hence $B\setminus A\in\mathcal{L}$
$\{A_i\}_{i=1}^\infty$ are pairwise disjoint and $A_i\in\mathcal{L}$ $\begin{aligned} \mu_1(\bigcup_{i=1}^\infty A_i)=\sum_{i=1}^\infty \mu_1(A_i)&=\sum_{i=1}^\infty\mu_2(A_i)\\ &=\mu_2(\bigcup_{i=1}^\infty A_i) < \infty \end{aligned}$ hence $\bigcup_{i=1}^\infty A_i\in\mathcal{L}$ .
$\mathcal{L}$ is a $\lambda$ -system！ $\square$

Proof ( $\sigma$ -Finite Measures)
For any $A\in\mathcal{A}$ s.t. $\mu_1(A)=\mu_2(A)<\infty$ , we define $\mathcal{L}_A$ to be all $B\subseteq\Omega$ s.t. $\mu_1(A\cap B)=\mu_2(A\cap B)$ .
Proceeding as in the proof above, we can show that $\mathcal{L}_A$ is a $\lambda$ -system and thus $\sigma(A)\subset\mathcal{L}_A ~ \forall A\in\mathcal{A}$ .
By $\sigma$ -Finiteness we decompose $\Omega=\bigcup_{i=1}^\infty A_i$ , $A_i\in\mathcal{A}$ and $\mu_1(A_i)=\mu_2(A_i) < \infty$ . For any $B\in\sigma(\mathcal{A})$ and any $n\in\mathbb{N}$
$\mu_1\left(\bigcup_{i=1}^n(B\cap A_i)\right)=\sum_{i=1}^n \mu_1(B\cap A_i)-\sum_{i < j}\mu_1(B\cap A_i \cap A_j) + \cdots$
here we use inclusion-exclusion formula. This also works for $\mu_2$ .
Since $\mathcal{A}$ is a $\pi$ -system, $A_i\cap A_j\in\mathcal{A}$ as well as futher intersections, thus
$\mu_1\left(\bigcup_{i=1}^n(B\cap A_i)\right)=\mu_2\left(\bigcup_{i=1}^n(B\cap A_i)\right) ~\forall n\in\mathbb{N}$
Let $n\rightarrow\infty$ we get $\mu_1(B)=\mu_2(B)~ \forall B\in\sigma(\mathcal{A})$ $\square$

Borel $\sigma$ -Field#

Definition
$\mathcal{B}(\mathbb{R})=\sigma(\text{open sets in }\mathbb{R})$

Lebesgue Measure#

Definition
For any interval $(a,b]$ in $\mathbb{R}$ , the Lebesgue measure is defined as $\lambda((a,b])=b-a$ .

Are there any $A\subset \mathscr{P}(\Omega)$ s.t. $A$ is not $\lambda$ -measurable? No

Example: Vitali Set
Let $\Omega=(0, 1]$ , for $x,y \in (0,1]$ define addition mod $1$
$x+y= \begin{cases} x+y & \text{if } x+y\leq 1 \\ x+y-1 & \text{if } x+y>1 \end{cases}$
Define $\mathcal{L}$ to contain all $\lambda$ -measureable sets $A\subseteq (0,1]$ s.t. $\lambda(A)=\lambda(A+x)$ for any $x \in (0,1]$ , where $A+x=\{x+y\in(0,1] : y \in A\}$ (shift $A$ by $x$ ) then we claim that $\mathcal{L}$ is a $\lambda$ -system.
Since $\mathcal{A}$ is the set contains all intervals $(a, b]\subseteq \Omega$ , we have $\mathcal{A} \subset \mathcal{L}$ because $\lambda((a, b])=b-a$ and $\lambda((a, b]+x)=\lambda((a+x, b+x])=b-a$ .
By Dynkin $\pi$ - $\lambda$ Theorem, $\sigma(\mathcal{A})=\mathcal{B}\subset\mathcal{L}$
i.e. Every Borel subset of $(0, 1]$ is shift invariant w.r.t $\lambda$
Next, we say that $x\sim y$ if $x-y\in\mathbb{Q}$ then we can decompose $(0, 1]$ into disjoint Equivalence classes.
Define $H\subset (0,1]$ s.t. $H$ contains one element from each equivalence class. (We can do this because of the Axiom of Choice) Then no two points in $H$ are equivalent. i.e. $r_1, r_2\in\mathbb{Q}$ then $(H+r_1)\cap(H+r_2)=\varnothing$ for $r_1\neq r_2$
Thus $(0, 1]=\bigcup_{r\in\mathbb{Q}}(H+r)$ and by countably additivity
$1 = \lambda((0, 1]) = \sum_{r\in\mathbb{Q}}\lambda(H+r)$
since $\lambda$ is traslation invariant, $\lambda(H+r_1)=\lambda(H+r_2)=\lambda(H)$ .
If $\lambda(H)=0$ , then $1=\sum_{r\in\mathbb{Q}}\lambda(H)=0$ .
If $\lambda(H)>0$ , then $1=\sum_{r\in\mathbb{Q}}\lambda(H)=\infty$
which yields a contradiction. Thus $H$ is not $\lambda$ -measurable and we call it Vitali Set.
Fun fact: Lebesgue Measure on $\mathbb{R}$ is the only translation invariant measure.
Same for $\mathbb{R}^n$
There is no $\infty$ -dimensional Lebesgue Measure. i.e. No traslation invariant measure.

Product Measure#

Definition
For two Measure Spaces $(\mathbb{X}, \mathcal{X}, \mu)$ and $(\mathbb{Y}, \mathcal{Y}, \nu)$ , define $(\mathbb{X}\times\mathbb{Y}, \mathcal{X}\times\mathcal{Y}, \pi)$ where $\pi(A\times B)=\mu(A)\nu(B)$ for $A\in\mathcal{X}$ and $B\in\mathcal{Y}$ .

Question : How are these related? $\mathcal{B}(\mathbb{X})\times\mathcal{B}(\mathbb{Y})$ and $\mathcal{B}(\mathbb{X}\times\mathbb{Y})$

From Dudley 4.1.7 $\mathcal{B}(\mathbb{X})\times\mathcal{B}(\mathbb{Y})\subset\mathcal{B}(\mathbb{X}\times\mathbb{Y})$ , but these two are “usually” equal to each other. e.g. $\mathbb{X}=\mathbb{Y}=\mathbb{R}$

Independence#

Independence for sets
For a countable collection of sets $A_i, i\in \mathcal{I}$ , we say that the collection is independent if for all finite subsets $J \subset I$ , we have
$\mu\left(\bigcap_{j\in \mathcal{J}}A_j\right)=\prod_{j\in \mathcal{J}}\mu(A_j)$

Independence for $\sigma$ -Fields
For a countable collection of $\sigma$ -Fields $F_i \subset F, i \in \mathcal{I}$ , we say that this collection of $\sigma$ -Fields is independent if any set of sets $\{A_i \in F_i : i \in \mathcal{I}\}$ is independent in the sense of the previous definition

Theorem
Let $A_1, A_2 \subset F$ be $\pi$ -systems. If $\mu(A_1 \cap A_2) = \mu(A_1)\mu(A_2)$ for any $A_1 \in \mathcal{A}_1$ and $A_2 \in \mathcal{A}_2$ , then $\sigma(A_1)$ and $\sigma(A_2)$ are independent.

Proof
For a fixed $A_1 \in \mathcal{A}_1$ , we can define two measures for $B \in \mathcal{F}$ as
$\nu_1(B) = \mu(A_1 \cap B) ~~\text{and}~~ \nu_2(B) = \mu(A_1)\mu(B).$
By assumption, $\nu_1(A_2) = \nu_2(A_2)$ for any $A_2 \in \mathcal{A}_2$ . Hence, by Uniqueness of Extension Theorem, they must coincide on $\sigma(A_2)$ . Therefore, $\mu(A_1 \cap B_2) = \mu(A_1)\mu(B_2)$ for a fixed $A_1$ and any $B_2 \in \sigma(A_2)$ .
This argument can be repeated by fixing an element $B_2 \in \sigma(A_2)$ to get that $\mu(B_1 \cap B_2) = \mu(B_1)\mu(B_2)$ for $B_i \in \sigma(A_i), i=1,2$ . $\square$

Functions, Random Variables and Integration#

Simple Functions and Random Variables#

Simple Random Variable
Let $(\Omega, \mathcal{F}, P)$ be a Probability Space i.e. $P(\Omega)=1$ . A simple random variable $X : \Omega\rightarrow\mathbb{R}$ is a real valued function that only takes on a finite number of values $x_1, \dots , x_p$ and such that the set
$\{\omega\in\Omega : X(\omega)=x_i\}\in\mathcal{F}$

One way to write such a function is to finitely partition $\Omega$ into disjoint sets $\{A_i\}_{i=1}^p$ i.e. $\bigcup_{i=1}^p A_i=\Omega$ and $A_i\cap A_j=\varnothing$ and write

X(\omega) = \sum_{i=1}^px_i \mathbf{1}[\omega\in A_i]

Then we can say that the probability that $X$ is equal to $x_i$ is

P(X=x_i)=P(\{\omega\in\Omega : X(\omega)=x_i\})=P(A_i)

Furthermore, this allows us to define the expectation of the simple random variable $X$ to be

\mathbb{E}X = \sum_{i=1}^p x_iP(X=x_i)

Simple Measurable Function
Let $(\Omega, \mathcal{F}, \mu)$ be a Probability Space. A simple function $F:\Omega\rightarrow\mathbb{R}$ is s.t.
$F(\omega)=\sum_{i=1}^p x_i\mathbf{1}[\omega\in B_i]~~ ~B_i\in\mathcal{F}$
which is the linear combination of indicator functions. The sets $B_i$ need not be disjoint, but given a simple function, we can define it in terms of disjoint $B_i$ .

Then, we define the integral of a simple function to be

\int F\mathrm{d}\mu \vcentcolon= \sum_{i=1}^p x_i\mu(B_i)

Measurable Functions and Random Variables#

To extend the above idea of a simple random variable, we want to replace the finite $x_i$ with any Borel set $\mathcal{B} \subset \mathbb{R}$ . We need two Measureable Spaces $(\mathbb{X}, \mathcal{X})$ and $(\mathbb{Y}, \mathcal{Y})$ .

Measurable Function
A function $f : \mathbb{X}\rightarrow\mathbb{Y}$ is said to be measurable (with respect to $\mathcal{X}/\mathcal{Y}$ ) if $f^{-1}(B)\in\mathcal{X}$ for any $B\in\mathcal{Y}$ . If $\mathbb{Y}=\mathbb{R}$ , then we say that $f$ is a $\mathcal{X}$ -measurable.

Typically, the $\sigma$ -Fields of interest are the Borel $\sigma$ -Fields and it is sometimes writen as $(\mathbb{X}, \mathcal{B}(\mathbb{X}))$ when we have a topological space. Moreover, the space $(\mathbb{X}, \mathcal{X})$ is typically taken to be $(\mathbb{R}, \mathcal{B}(\mathbb{R}))$ or $(\mathbb{R}^+, \mathcal{B}(\mathbb{R}^+))$ . In this case, we say that $f$ is Borel Measurable.

If we replace $\mathcal{B}(\mathbb{R})$ with $\mathcal{M}_λ(\mathbb{R})$ , the set of Lebesgue measurable subsets of $\mathbb{R}$ , then we say $f$ is Lebesgue Measurable.

Cool facts about Measurable Functions#

Inverse images of set functions preserve set operations. i.e. for $f:\mathbb{X}\rightarrow\mathbb{Y}$ and $A, A_i\subset\mathbb{Y}, i\in \mathcal{I}$ ,
$f^{-1}\left(\bigcup_{i\in \mathcal{I}} A_i\right) = \bigcup_{i\in \mathcal{I}} f^{-1}(A_i) ~~ \text{and} ~~ f^{-1}(\mathbb{Y}\setminus A) = \mathbb{X} \setminus f^{-1}(A)$
For a measurable set function $f$ , this implies that $\{f^{-1}(B) : B \in \mathcal{Y}\}$ is a $\sigma$ -Field and is contained in $\mathcal{X}$ . Hence, we want $\mathcal{Y}$ to be no larger than $\mathcal{X}$ to have measurable functions. Furthermore, this can be used to show that the measurability of $f$ can be established by looking only at a collection of sets $\mathcal{A} \subset \mathcal{Y}$ that generates $\mathcal{Y}$ .
Example
let $\mathcal{A}$ be the set of all half-lines $A_t = (−\infty, t]$ for $t \in \mathbb{R}$ will generate $\mathcal{B}(\mathbb{R})$ . Thus, $f$ is measurable as long as the sets $\{x : f(x) \leq t\}$ are measurable.
For any $A \in \mathcal{X}$ , the indicator functions $f(x) = \mathbf{1}[x \in A]$ are measurable. The $\sigma$ -Field generated by $f^{−1}$ is simply $\{\varnothing, A, A^c, \mathbb{X}\}\subset\mathcal{X}$ .
For measurable functions $f, g : \mathbb{X} \rightarrow \mathbb{R}$ , the functions $f + g$ and $fg$ are measurable.
For measurable functions, $\{f_i\}_{i=1}^\infty$ from $\mathbb{X}$ to $\mathbb{R}$ , the following are also measurable: $\sup_i f_i$ , $\inf_i f_i$ , $\limsup_i f_i$ , $\liminf_i f_i$ and $\lim_i f_i$ if it exists.
Proof
In set notation, $\{x : \sup_i f_i(x)\leq t\}=\bigcap_{i=1}^\infty\{x : f_i(x)\leq t\}$ where the righthand side is a countable intersection of measurable sets and hence measurable. Similarly, $\{x : \inf_i f_i(x)\leq t\}=\bigcup_{i=1}^\infty\{x : f_i(x)\leq t\}$ and $\limsup_i f_i = \inf_i \sup_{j\geq i} f_i$ and $\liminf_i f_i = \sup_i\inf_{j\geq i} f_i$ . If $\lim_i f_i$ exists then $\limsup f_i=\lim_i f_i=\liminf_i f_i$ . $\square$
Let $f : \mathbb{X}\rightarrow\mathbb{R}$ be a continuous function, then it is measurable.
Proof
If $U$ is an open set in $\mathbb{R}$ , then $f^{−1}(U)$ is open in $\mathbb{X}$ (definition of a continous function between two topological spaces). Thus, the set $f^{−1}(U)$ is measurable. Since the open sets of $\mathbb{R}$ generate $\mathcal{B}(\mathbb{R})$ , the function $f$ is measurable. $\square$
Given a collection of functions $f_i: \mathbb{X}\rightarrow\mathbb{Y}, i\in \mathcal{I}$ , we can make them measurable by constructing the measurable space $(\mathbb{X},\mathcal{X})$ where $\sigma(\{f_i\}_{i\in \mathcal{I}})\subseteq\mathcal{X}$ is the $\sigma$ -field generated by the sets $f^{-1}_i(B)$ for all $i$ and $B\in\mathcal{Y}$ .

Almost Surely / Almost Everywhere
Let $(\Omega, \mathcal{F}, \mu)$ be a measure space. For two functions $f, g : \Omega\rightarrow\mathbb{R}$ , we say that $f = g$ a.e. (almost everywhere) when the set $N = \{\omega : f(\omega) \neq g(\omega)\}$ has measure $\mu(N) = 0$ .
In probability theory, “almost everywhere” is replaced with “almost surely” abbreviated a.s. and it is equivalently is written “with probability 1” or w.p.1.

Example
Let $([0, 1], \mathcal{B}, \lambda)$ be the standard measure space of Borel sets on the unit interval with Lebesgue measure. Let $f(t)=0$ for all $t\in(0,1]$ and $g(t) = 0$ on $(0, 1]\setminus\mathbb{Q}$ and $g(t)=1$ on $(0, 1]\cap\mathbb{Q}$ .
Then we have $f=g$ a.e. that is $\lambda((0, 1)\cap\mathbb{Q}) = 0$ . To prove that $\lambda(\mathbb{Q})=0$ , we enumerate each rational number $\{q_m\}_{m=1}^\infty$ and surround each $q_m$ with an interval $(q_m-\frac{\epsilon}{2^m}, q_m + \frac{\epsilon}{2^m})$ . For $\epsilon > 0$ , $\sum_{m=1}^\infty \lambda((q_m-\frac{\epsilon}{2^m}, q_m + \frac{\epsilon}{2^m}))=\sum_{m=1}^\infty\frac{\epsilon}{2^{m-1}}=2\epsilon$ . Since $\epsilon$ is arbitrary, we have $\lambda(\mathbb{Q})=0$ .

Integration#

We will consider measurable functions mapping from $(\Omega, \mathcal{F})$ to $[-\infty, \infty]$ , which is called the extended real line. This allows us to handle sets such as $f^{-1}(\infty)$ .

Notation : $f_i\uparrow f$
We use $f_i\uparrow f$ to represent a sequence of functions $\{f_i\}$ that are increasing and converge to $f$ for every $\omega$ . This implies that $f_i(\omega)\rightarrow f(\omega)$ and $f_i(\omega)\leq f_{i+1}(\omega)$ for all $\omega$ .

Theorem
Let $(\Omega, \mathcal{F})$ be a measurable space and $\mathcal{A}$ a $\pi$ -system that generates $\mathcal{F}$ ( $~\sigma(\mathcal{A})=\mathcal{F}~$ ). Let $\mathcal{V}$ be a linear space that contains
all indicators $\mathbf{1}_\Omega$ and $\mathbf{1}_A$ for each $A\in\mathcal{A}$
all functions $f$ such that $\exists f_i\in\mathcal{V}$ s.t. $f_i\uparrow f$
Then $\mathcal{V}$ contains all measurable functions.

Proof
First, $\mathbf{1}_A\in\mathcal{A}$ . Let $\mathcal{L}=\{B\in\mathcal{F} : \mathbf{1}_B\in\mathcal{V}\}$ , we claim that $\mathcal{L}$ is a $\lambda$ -system. Since $\mathcal{A}\subset\mathcal{L}$ , by Dynkin $\pi$ - $\lambda$ Theorem, $\sigma(\mathcal{A})\subseteq\mathcal{L}$ . By the definition of $\mathcal{L}$ , we have that $\mathcal{V}\subseteq\mathcal{F}$ , thus $\mathcal{L}=\mathcal{F}$ , so every indicator function $\mathbf{1}_B$ is in $\mathcal{V}$ .
Let $f$ be a non-negative measurable function, we can define $f_i=2^{-i}\lfloor2^if\rfloor$ . Each $f_i$ is a finite linear combination of indicator functions and hence $f_i \in \mathcal{V}$ . Furthermore, $f_i\uparrow f$ and thus $f\in\mathcal{V}$ .
Lastly, for a general measurable $f$ , we write $f=f^+-f^-$ where
$\begin{aligned} f^+(\omega)&= \begin{cases} f(\omega) & \text{if } f(\omega)\geq 0 \\ 0 & \text{otherwise} \end{cases} \\ f^-(\omega)&= \begin{cases} -f(\omega) & \text{if } f(\omega)< 0 \\ 0 & \text{otherwise} \end{cases} \end{aligned}$
which are both non-negative measurable functions. $\square$

Integral of a Measurable Function
For a non-negative measurable function $f : \Omega\rightarrow [0,\infty]$ on the measure space $(\Omega, \mathcal{F}, \mu)$ , we define
$\int f\mathrm{d}\mu = \sup\left[\sum_{i\in \mathcal{I}} \left\{\inf_{\omega\in A_i} f(\omega) \right\}\mu(A_i)\right]$
where the supremum is taken over all finite partitions $\{A_i\}_{i\in \mathcal{I}}$ of $\Omega$ .

Inside the square brackets is the integral of the simple function that assigns a value of $\inf_{\omega\in A_i} f(\omega)$ for the set A_i. Hence, for a non-negative $f$ , we consider all simple functions $g$ such that $0 \leq g \leq f$ and define the integral to be the supremum of the integral of $g$ . To extend this to all measurable functions $f$ , we write $f=f^+-f^-$ then

\int f\mathrm{d}\mu = \int f^+\mathrm{d}\mu - \int f^-\mathrm{d}\mu

Monotone Convergence Theorem for Simple Functions
Let $(\Omega, \mathcal{F}, \mu)$ be a measure space, and let $f \geq 0$ be measureable, and $f_n \geq 0~\forall n \in \mathbb{N}$ be a sequence of measureable simple functions such that $f_n \uparrow f$ . Then, $\int f_n\mathrm{d}\mu\uparrow\int f\mathrm{d}\mu$ .

Proof
Since $f_n \uparrow f$ and $f$ is integrable, then $\int f_n\mathrm{d}\mu \uparrow c\in[0,\infty)$ and $c\leq \int f\mathrm{d}\mu$ . To prove the other side of the inequality, let $g$ be any simple measureable function s.t. $0\leq g\leq f$ . Our goal is to show that $\int g\mathrm{d}\mu\leq c$ as this will imply that $c\geq \int f\mathrm{d}\mu$ .
First, we write $g=\sum_{i\in \mathcal{I}}a_i \mathbf{1}_{A_i}$ where $A_i$ are disjoint partition of $\Omega$ and similarly $f_n=\sum_{j\in \mathcal{J}} b_j^{(n)} \mathbf{1}_{B_j^{(n)}}$ . Consequently,
$f_n = \sum_{i\in \mathcal{I}} f_n \mathbf{1}_{A_i}=\sum_{i, j} b_j^{(n)} \mathbf{1}_{A_i\cap B_j^{(n)}}$
and $\int f_n\mathrm{d}\mu=\sum_{i\in\mathcal{I}}\int_{A_i}f_n\mathrm{d}\mu$ . Hence, we want to show that for each $i \in \mathcal{I}$ that
$\lim_{n\rightarrow \infty}\int_{A_i}f_n\mathrm{d}\mu\geq \int_{A_i} g\mathrm{d}\mu = a_i\mu(A_i)$
First, if $a_i=0$ , then the eqaulity above must hold. If $a_i>0$ , we can divide by $a_i$ and without loss of generality, we take $a_i=1$ and consider $g=\mathbf{1}_A$ for some set $A$ .
For any $\epsilon>0$ , let $C_n=\{x\in A : f_n(x) > 1 - \epsilon\}$ . Then $C_n\uparrow A$ , which means
$C_1\subseteq C_2\subseteq \cdots \subseteq A ~~\text{ and }~ \bigcup_{n=1}^\infty C_n = A$
By countable additivity of $\mu$
$\mu(C_{n+1}) = \mu(C_1) + \sum_{i=1}^n \mu(C_{i + 1} \setminus C_i)$
and $\mu(C_n)\uparrow \mu(A)$ . Since $\int f_n\mathrm{d}\mu \geq (1 - \epsilon)\mu(C_n)$ , we have that $c\geq (1 - \epsilon)\mu(A) = (1 - \epsilon)\int g\mathrm{d}\mu$ . Take $\epsilon$ to zero gives $c\geq \int g\mathrm{d}\mu$ . $\square$

Theorem
Let $(\Omega, \mathcal{F}, \mu)$ be a measure space, and let $f, g : \Omega \rightarrow [-\infty, \infty]$ be measureable and $f = g$ a.e. Then, $f$ is integrable if and only if $g$ is integrable. If $f$ and $g$ are integrable, then $\int f\mathrm{d}\mu = \int g\mathrm{d}\mu$ .

Proof
Let $f = g$ on $\Omega \setminus N$ where $\mu(N) = 0$ . For any measureable function $h : \Omega \rightarrow [-\infty, \infty]$ , we can consider when $\int_\Omega h\mathrm{d}\mu = \int_{\Omega\setminus N} h\mathrm{d}\mu$ coincide.
True if $h$ is an indicator function because $\mu(A) = \mu(A\setminus N)$
Also true for $h$ being a non-negative simple function.
From MCT for Simple Functions, we can take non-negative simple functions $h$ to any non-negative measureable function.
Lastly, write $\int h\mathrm{d}\mu = \int h^+\mathrm{d}\mu - \int h^-\mathrm{d}\mu$ shows that the integrals will coincide for any integrable measureable function.
To complete the proof, we note that
$\int f\mathrm{d}\mu = \int_{\Omega\setminus N}f \mathrm{d}\mu = \int_{\Omega\setminus N}g \mathrm{d}\mu = \int g\mathrm{d}\mu$
This result basically tells us that we can modify functions on a set of measure zero without breaking anything. $\square$

Monotone Convergence Theorem#

Monotone Convergence Theorem
Let $(\Omega, \mathcal{F}, \mu)$ be a measure space and let $\{f_i\}_{i=1}^\infty$ be measurable functions from $\Omega$ to $[-\infty, \infty]$ such that $f_i \uparrow f$ $\mu$ -a.e. and $\int f_1\mathrm{d}\mu > -\infty$ . Then $\int f_i\mathrm{d}\mu \uparrow \int f\mathrm{d}\mu$ . (This means that we can swap the limit and the integral)

Proof
First, we need to check that $f$ is measureable. For $c\in\mathbb{R}$ , we consider the sets $(c, \infty]$ , which generate the Borel $\sigma$ -Field. Since $f_i\uparrow f$ , $f^{-1}((c, \infty]) = \bigcup_{i=1}^\infty f_i^{-1}((c, \infty])$ and $f_i^{-1}((c, \infty]) \in \mathcal{F}$ , thus $f$ is measureable. (by the first cool fact about measurable functions)
Next, assume that $f_1 \geq 0$ , and for each $f_i$ we take simple functions $g_{ij}$ such that $g_{ij} \uparrow f_i$ as $j\rightarrow\infty$ . Thus, by MCT for Simple Functions, $\int g_{ij}\mathrm{d}\mu\uparrow\int f_i\mathrm{d}\mu$ . Furthermore, let $g_i^* = \max\{g_{1i}, \cdots , g_{ii}\}$ . These $g_i^*$ are simple functions and $g_i^*\uparrow f$ . Once again, MCT for Simple Functions implies that $\int g_i^*\mathrm{d}\mu\uparrow\int f\mathrm{d}\mu$ . But since $g_i^* \leq f_i$ by construction, $\int g_i^*\mathrm{d}\mu \leq \int f_i\mathrm{d}\mu \leq \int f\mathrm{d}\mu$ . Thus, $\int f_i\mathrm{d}\mu\uparrow\int f\mathrm{d}\mu$ . This means we are done for non-negative fucntions ( $f_1\geq 0$ ).
Now, we assume that $f \leq 0$ . In this case $f_i \uparrow f$ implies that $−f_i \downarrow −f$ . Let $h=-f$ and $h_i=-f_i$ , we have $0\leq \int h\mathrm{d}\mu\leq \int h_i\mathrm{d}\mu$ . Next, note that $0\leq h_1-h_i\uparrow h_1-h$ . Applying the above result gives that $\int (h_1-h_i)\mathrm{d}\mu\uparrow \int (h_1-h)\mathrm{d}\mu$ . Since all of the $h$ have finite integrals, we are allowed to subtract to get that $\int h_i\mathrm{d}\mu\downarrow\int h\mathrm{d}\mu$ and thus $\int f_i\mathrm{d}\mu\uparrow\int f\mathrm{d}\mu$ .
For a general function $f = f^+ - f^-$ , we have $f_i^+\uparrow f^+$ and $f_i^-\downarrow f^-$ and $\int f^-\mathrm{d}\mu < \infty$ . So by the above special cases, $\int f_i^+\mathrm{d}\mu\uparrow\int f^+\mathrm{d}\mu$ and $\int f_i^-\mathrm{d}\mu\downarrow\int f^-\mathrm{d}\mu$ . Finally, $\int f_i\mathrm{d}\mu \uparrow \int f\mathrm{d}\mu$ . $\square$
We only require $f_i \uparrow f$ to hold almost everywhere to establish the result. Hence convergence can fail on a set of measure (probability) zero and we still have convergence of the integrals.
Secondly, we can redo the above proof for $f_i \downarrow f$ with $\int f_1\mathrm{d}\mu < \infty$ to get a similar result for decreasing sequence.

Fatou’s Lemma #

Fatous’ Lemma
Let $(\Omega, \mathcal{F}, \mu)$ be a measure space and let $\{f_i\}_{i=1}^\infty$ be non-negative measurable functions from $\Omega$ to $[-\infty, \infty]$ . Then, $\int \liminf f_i\mathrm{d}\mu \leq \liminf \int f_i\mathrm{d}\mu$

Proof
Recall that $\liminf_{i\rightarrow\infty} = \sup_j \inf_{i>j} f_i$ . Hence, let $g_j=\inf_{i\geq j} f_i$ . Then, $g_j\uparrow \liminf_{i\rightarrow\infty} f_i$ and $f_1\geq 0$ by assumption. So MCT for Simple Functions says that $\int g_j\mathrm{d}\mu\uparrow\int\liminf_{i\rightarrow\infty}f_i\mathrm{d}\mu$ . By construction, $g_j\leq f_i$ for any $i\geq j$ , thus $\int g_j\mathrm{d}\mu \leq \int f_i\mathrm{d}\mu$ for any $i\geq j$ and subsequently, $\int g_j\mathrm{d}\mu\leq \inf_{i\geq j}\int f_i\mathrm{d}\mu$ . Taking $j\rightarrow\infty$ gives $\lim_{j\rightarrow\infty}\int g_j\mathrm{d}\mu = \int\liminf f_i\mathrm{d}\mu\leq\liminf\int f_i\mathrm{d}\mu$ . $\square$

Dominated Convergence Theorem#

Dominated Convergence Theorem
Let $(\Omega, \mathcal{F}, \mu)$ be a measure space and let $\{f_i\}_{i=1}^\infty$ and $g$ be measurable functions and absolutely integrable. If $|f_i| \leq g$ for all $i$ and $f_i(\omega) \rightarrow f(\omega)$ for each $\omega \in \Omega$ (i.e. pointwise convergence), then $f$ is absolutely integrable and $\int f_i\mathrm{d}\mu \rightarrow \int f\mathrm{d}\mu$ .

Proof
Let $f_i^\wedge = \inf_{j\geq i} f_j$ and $f_i^\vee = \sup_{j\geq i} f_j$ . Then $f_i^\wedge \leq f_i \leq f_i^\vee$ . We have that $f_i^\wedge\uparrow f$ and $\int f_1^\wedge\mathrm{d}\mu\geq -\int g\mathrm{d}\mu > -\infty$ . So MCT for Simple Functions implies that $\int f_i^\wedge\mathrm{d}\mu\uparrow \int f\mathrm{d}\mu$ .
Do the same for $f_i^\vee$ , we have that $f_i^\vee\downarrow f$ and hence that $\int f_i^\vee\mathrm{d}\mu\downarrow\int f\mathrm{d}\mu$ . Since $\int f_i^\wedge\mathrm{d}\mu\leq \int f_i\mathrm{d}\mu\leq \int f_i^\vee\mathrm{d}\mu$ , we have the desired result that $\int f_i\mathrm{d}\mu\rightarrow \int f\mathrm{d}\mu$ . $\square$

Lebesgue-Stieltjes Measure#

Let $(\mathbb{X}, \mathcal{X})$ and $(\mathbb{Y}, \mathcal{Y})$ be two measurable spaces. Let $\psi : \mathbb{X}\rightarrow\mathbb{Y}$ be a measurable function and $\mu$ be a measure on $\mathcal{X}$ . Then we can define $\nu = \mu \circ \psi^{-1}$ to be a measure of $\mathcal{Y}$ . This allows us to turn Lebesgue measure into Lebesgue-Stieltjes measures.

Theorem
Let $F : \mathbb{R} \rightarrow \mathbb{R}$ be non-constant, right-continuous, and non-decreasing. Then, there exists a unique measure $\mathrm{d}F$ on $\mathbb{R}$ such that for all $a, b \in \mathbb{R}$ with $a < b$ ,
$\mathrm{d}F((a, b]) = F(b) - F(a)$

Proof
Let $F(\infty) = \lim_{x\rightarrow\infty} F(x)$ and $F(-\infty) = \lim_{x\rightarrow-\infty}F(x)$ . We define an open interval $I = (F(-\infty), F(\infty))$ and define $g(y) = \inf\{x\in\mathbb{R} : y\leq F(x)\}$ . We want to define $\mathrm{d}F$ to be $\lambda \circ g^{−1}$ where $\lambda$ is Lebesgue Measure on $\mathbb{R}$ , so we need to show that this makes sense.
We first show that $g$ is left-continuous and non-decreasing and for $y \in I$ and $x \in \mathbb{R}, g(y) \leq x$ if and only if $y \leq F(x)$ . To show this, fix a $y\in I$ and let $J_y = \{x\in\mathbb{R} : y\leq F(x)\}$ . As $F$ is non-decreasing, if $x\in J_y$ and $x'\geq x$ then $x'\in J_y$ . As $F$ is right-continuous, if $x_n\in J_y$ and $x_n\downarrow x$ then $x\in J_y$ . Therefore, $J_y = [g(y), \infty)$ and $g(y)\leq x$ if and only if $y\leq F(x)$ . Secondly, for $y\leq y'$ , we have that $J_{y'}\subseteq J_y$ and thus $g(y)\leq g(y')$ . So if $y_n\uparrow y$ , then $J_y = \bigcap_{n=1}^\infty J_{y_n}$ and thus $g(y_n)\rightarrow g(y)$ , which implies that $g$ is left continuous and non-decreasing.
From the above, $g$ is Borel Measurable and thus defining $\mathrm{d}F = \lambda \circ g^{-1}$ gives us that
$\mathrm{d}F((a, b]) = \lambda(\{y : g(y) > a, g(y) \leq b\}) = \lambda((F(a), F(b)]) = F(b) - F(a)$
Furthermore, this measure, $\mathrm{d}F$ , is unique by using the same arguments as before for Lebesgue Measure. $\square$
In the case that $F : \mathbb{R} \rightarrow [0, 1]$ such that the interval $I = [0, 1]$ , we have a cumulative distribution function, which induces a measure on the real line. This allows us to do things like integrate with respect to such measures——i.e. take an expectation.

Radon Measure#

Definition
Let $(\Omega, \mathcal{B}, \mu)$ be a measure space where $\mathcal{B}$ is the Borel $\sigma$ -field. The measure $\mu$ is said to be a Radon Measure if $\mu(K) < \infty$ for all compact $K \in \mathcal{B}$ .

$\mathrm{d}F$ is a Radon Measure.
Every non-zero Radon Measure on $\mathcal{B}(\mathbb{R})$ can be written as $\mathrm{d}F = \lambda \circ g^{−1}$ for some $F$ .
If $\mu$ is a Radon Measure on $\mathbb{R}$ , then we can define $F$ as
$F(x) = \begin{cases} \mu((0, x]) & \text{if } x > 0 \\ -\mu((x, 0]) & \text{if } x < 0 \\ \end{cases}$
Thus, $F(b) − F(a) = \mu((a, b])$ for $a < b$ and hence $\mu = \mathrm{d}F$ by uniqueness.

Product Measure#

Definition
Given two $\sigma$ -fields $\mathcal{X}$ and $\mathcal{Y}$ , we define the product $\sigma$ -field to be $\mathcal{X} \times \mathcal{Y}$ , which is the $\sigma$ -filed generated by the rectangle $A\times B$ where $A\in\mathcal{X}$ and $B\in\mathcal{Y}$ . The collection of all rectangles will be denoted as $\mathcal{R}$

Monotone Class#

Definition
A collection of subsets $\mathcal{M}$ of $\Omega$ is said to be monotone if
for $\{A_i\}_{i=1}^\infty$ s.t. $A_i \in \mathcal{M}$ and $A_i \uparrow A = \bigcup_{i=1}^\infty Ai$ , then $A \in \mathcal{M}$ .
for $\{A_i\}_{i=1}^\infty$ s.t. $A_i \in \mathcal{M}$ and $A_i \downarrow A = \bigcup_{i=1}^\infty Ai$ , then $A \in \mathcal{M}$ .

Note that if a field $\mathcal{A}$ is also monotone, then it is a $\sigma$ -field (by definition of $\sigma$ -field.)

Monotone Class Theorem
Let $\mathcal{A}$ be a field and $\mathcal{M}$ be monotone such that $\mathcal{A}\subset\mathcal{M}$ . Then, $\sigma(\mathcal{A}) \subseteq \mathcal{M}$

Proof
This proof is similar to the one of Dynkin $\pi$ - $\lambda$ Theorem.

Existence and Uniqueness of Product Measure#

Existence and Uniqueness Theorem of Product Measure
Let $(\mathbb{X}, \mathcal{X} , \mu)$ and $(\mathbb{Y}, \mathcal{Y}, \nu)$ be $\sigma$ -finite measure spaces. We denote the product $\sigma$ -Field to be $\mathcal{X} \times \mathcal{Y}$ . (the cartesian product of two $\sigma$ -Fields may not be a $\sigma$ -Field) Let $π$ be a set function on $\mathcal{X}\times\mathcal{Y}$ such that for $A \in \mathcal{X}$ and $B \in \mathcal{Y}$ , $π(A \times B) = \mu(A)\nu(B)$ . Then, $π$ extends uniquely to a measure on $(\mathbb{X} \times \mathbb{Y}, \mathcal{X}\times\mathcal{Y})$ such that for any $E \in \mathcal{X} \times \mathcal{Y}$ ,
$\pi(E) = \int\int \mathbf{1}_E(x, y)\mathrm{d}\mu(x)\mathrm{d}\nu(y) = \int\int \mathbf{1}_E(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x)$

Lemma
Let $(\mathbb{X}, \mathcal{X} , \mu)$ and $(\mathbb{Y}, \mathcal{Y}, \nu)$ be finite measure spaces, and let
$\mathcal{F} = \left\{E \subset \mathbb{X}\times\mathbb{Y} : \int\int \mathbf{1}_E(x, y)\mathrm{d}\mu(x)\mathrm{d}\nu(y) = \int\int \mathbf{1}_E(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x)\right\}$
Then $\mathcal{X}\times\mathcal{Y} \subseteq \mathcal{F}$ . ( This means that $(\mathbb{X}\times\mathbb{Y}, \mathcal{X}\times\mathcal{Y}) \equiv (\mathbb{Y}\times\mathbb{X}, \mathcal{Y}\times\mathcal{X})~$ )

Proof
Let $E = A \times B$ for $A \in \mathcal{X}$ and $B \in \mathcal{Y}$ , i.e. $E \in \mathcal{R}$ . Then,
$\begin{aligned} \int\int \mathbf{1}_E(x, y)\mathrm{d}\mu(x)\mathrm{d}\nu(y) &=\mu(A) \int \mathbf{1}_B(y)\mathrm{d}\nu(y) \mu(A)\nu(B) =\nu(B)\mu(A)\\ &=\nu(B) \int \mathbf{1}_A(x)\mathrm{d}\mu(x) =\int\int \mathbf{1}_E(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x) \end{aligned}$
Therefore, $\mathcal{R} \subset \mathcal{F}$ .
Also, for disjoint $R_1, R_2 \in \mathcal{R}$ , $\mathbf{1}_{R_1\cup R_2} = \mathbf{1}_{R_1} + \mathbf{1}_{R_2}$ . Hence, $\mathcal{F}$ contains finite disjoint unions of $\mathcal{R}$ . This implies that the field generated by the set of rectangles $\mathcal{A} \subset \mathcal{F}$ . (Dudley 3.2.3)
Next, consider $\{E_i\}_{i=1}^\infty, E_i\in\mathcal{F}$ . Then if $E_i\uparrow E$ , then MCT says
$\int\int \mathbf{1}_{E_i}(x, y)\mathrm{d}\mu(x)\mathrm{d}\nu(y) ~\big\uparrow \int\int \mathbf{1}_{E}(x, y)\mathrm{d}\mu(x)\mathrm{d}\nu(y)$
and
$\int\int \mathbf{1}_{E_i}(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x) ~\big\uparrow \int\int \mathbf{1}_{E}(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x)$
Thus, $E \in \mathcal{F}$ and the same holds if $E_i \downarrow E$ . Therefore, $\mathcal{F}$ is a monotone class. Finally, applying the Monotone Class Theorem shows that $\mathcal{X} \times \mathcal{Y} = \sigma(\mathcal{A}) \subset \mathcal{F}$ . $\square$

Proof : Existence and Uniqueness of Product Measure
First, we consider the case that $\mu$ and $\nu$ are finite measures and $\pi(A\times B) = \nu(A)\nu(B)$ . Then we extend to a set function
$\pi(E)\vcentcolon=\int\int \mathbf{1}_E(x, y)\mathrm{d}\mu(x)\mathrm{d}(y)$
for any $E\in \mathcal{X}\times\mathcal{Y}$ . The above lemma says that the definiton makes sense and the order of integration can be reversed for any $E \in \mathcal{X} \times \mathcal{Y}$ . Linearity of integral implies that $\pi$ is finitely additive. Apply MCT shows that $\pi$ is countably additive.. Thus, $\pi$ is a measure on $\mathcal{X} \times \mathcal{Y}$ .
To show that $\pi$ is unique, let $\rho$ be some other set function such that $\rho(A \times B) = \mu(A)\nu(B)$ for $A \times B \in \mathcal{R}$ . Let $\mathcal{M} = \{E \subset \mathbb{X} \times \mathbb{Y} : \pi(E) = \rho(E)\}$ . Then, $\mathcal{M}$ is a monotone class because for $E_i \uparrow E =\bigcup_{i=1}^\infty E_i$ , we can rewrite $E = \bigcup_{i=1}^\infty D_i$ where $D_1 = E_1$ and $D_i = E_i \setminus E_{i−1}$ for $i \geq 2$ are disjoint. So by countable additivity, $\pi(E)=\rho(E)$ and we can do the same for $E_i \downarrow E$ . Thus, by Monotone Class Theorem $\mathcal{X} \times \mathcal{Y} \subseteq \mathcal{M}$ . Therefore, $\pi$ is unique on $\mathcal{X} \times \mathcal{Y}$ for finite measures $\mu$ and $\nu$ .
Now let $\mu$ and $\nu$ be $\sigma$ -finite measures. Let $\{A_i\}_{i=1}^\infty$ and $\{B_i\}_{i=1}^\infty$ be disjoint partitions of $\mathbb{X}$ and $\mathbb{Y}$ , respectively, such that $\mu(A_i)<\infty$ and $\nu(B_i)<\infty$ . Then, for any $E \in \mathcal{X} \times \mathcal{Y}$ , we define $E_{ij} = E\cap (A_i\times B_j)$ . From the above finite measure case,
$\int\int \mathbf{1}_{E_{ij}}(x, y)\mathrm{d}\mu(x)\mathrm{d}\nu(y) = \int\int \mathbf{1}_{E_{ij}}(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x)$
Sum over all $i$ and $j$ and apply MCT again to get
$\pi(E) = \int\int \mathbf{1}_{E}(x, y)\mathrm{d}\mu(x)\mathrm{d}\nu(y) = \int\int \mathbf{1}_{E}(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x)$
Futhermore, Monotone convergence implies that $\pi$ is countably additive and hence a measure on $\mathcal{X}\times\mathcal{Y}$ . For any other measure $\rho$ such that $\rho(A \times B) = \mu(A)\nu(B)$ , countably additivity and uniqueness for finite measures implies that
$\pi(E) = \sum_{i,j}\pi(E_{i,j}) = \sum_{i,j}\rho(E_{i,j}) = \rho(E)$
Hence, the extension of $\pi$ to $\mathcal{X} \times\mathcal{Y}$ is unique. $\square$

Fubini-Toneli#

Fubini-Toneli Theorem
Let $(\mathbb{X}, \mathcal{X} , \mu)$ and $(\mathbb{Y}, \mathcal{Y}, \nu)$ be $\sigma$ -finite measure spaces, and let $f : \mathbb{X} \times \mathbb{Y} \rightarrow \mathbb{R}$ be measurable with respect to $\mathcal{X} \times \mathcal{Y}$ such that either $f\geq 0$ (non-negative) or $\int\int |f|\mathrm{d}(\mu\times\nu)<\infty$ (absolutely integrable). Then,
$\int\int f\mathrm{d}(\mu\times\nu) = \int\int f(x,y)\mathrm{d}\mu(x)\mathrm{d}\nu(y) = \int\int f(x,y)\mathrm{d}\nu(y)\mathrm{d}\mu(x)$
Also, $\int f(x, y)\mathrm{d}\mu(x)$ is $\mathcal{Y}$ -measurable and $\int f(x, y)\mathrm{d}\nu(y)$ is $\mathcal{X}$ -measurable.

Proof
We have this for indicator functions from Existence and Uniqueness Theorem of Product Measure and thus the result for simple functions as integrals are linear.
Then, applying MCT to simple functions gives us that the above holds for non-negative measureable functions.
Instead, assume $\int\int|f| \mathrm{d}(\mu\times\nu) < \infty$ . Then, we can write $f = f^+ - f^-$ and the above holds for $f^+$ and $f^-$ separately. i.e. $\int f^+(x, y)\mathrm{d}\mu(x) < \infty$ for $\nu$ -almost-every $y$ and $\int f^+(x, y)\mathrm{d}\nu(y) < \infty$ for $\mu$ -almost-every $x$ and similarly for $f^-$ . Therefore,
$\int |f|(x, y)\mathrm{d}\nu(y) = \int f^+(x, y)\mathrm{d}\nu(y) + \int f^-(x, y)\mathrm{d}\nu(y) < \infty ~~~(\mu-a.e.)$
and thus,
$\int f(x, y)\mathrm{d}\nu(y) = \int f^+(x, y)\mathrm{d}\nu(y) - \int f^-(x, y)\mathrm{d}\nu(y) ~~~(\nu-a.e.)$
As we only require finiteness to occur almost everywhere to have the integral exist, we can integrate both sides of the above with respect to $\mu$ to get
$\int\int f(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x) = \int\int f^+(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x) - \int\int f^-(x, y)\mathrm{d}\nu(y)\mathrm{d}\mu(x)$
Do the same swapping $\mu$ and $\nu$ to conclude the theorem. $\square$
The above theorem lets us swap the order of integration for the product of two measure spaces. This can be extended by induction to the finite product of $n$ measure spaces.

Probability Theory#

$L^p$ Spaces#

$L^p$ Space
Let $(\Omega, \mathcal{F}, \mu)$ be a measure space and $f : \Omega \rightarrow [−\infty, \infty]$ a measurable function, then we say $f \in L^p(\Omega,\mathcal{F}, \mu)$ , for $1 \leq p < \infty$ if
$\int |f|^p d\mu < \infty$
For $p = \infty$ , we say $f \in L^\infty(\Omega,\mathcal{F}, \mu)$ if $\inf \{t\in [-\infty, \infty] : |f| \leq t ~~\mu\text{-a.e.}\} < \infty$

This definition allows us to write down the $L^p$ norm, which is defined as:

\begin{aligned} ||f||_p &= \left(\int |f|^p d\mu\right)^{1/p} \quad \text{for} \quad 1 \leq p < \infty \\ ||f||_\infty &= \inf \{t\in [-\infty, \infty] : |f| \leq t ~~\mu\text{-a.e.}\} \\ &= \inf \{t\in [-\infty, \infty] : \mu(\{|f(x)| > t\}) = 0\} \end{aligned}

Markov / Chebyshev and Jensen’s Inequalities#

Markov’s Inequality
Let f be a non-negative measurable function and $t > 0$ . Then, denote $\{f > t\} \vcentcolon= \{\omega \in \Omega : f(\omega) > t\}$ ,
$\mu(\{f > t\}) \leq t^{-1} \int f \mathrm{d}\mu$

Proof
Noting that $t\mathbf{1}_{\{f>t\}} \leq f$ , then by monotonicity of the integral,
$t\mu(\{f > t\}) = \int t\mathbf{1}_{\{f>t\}} \mathrm{d}\mu \leq \int f \mathrm{d}\mu$
which proves the theorem. $\square$

There are two useful ways to use Markov’s inequality:

Chebyshev’s Inequality: For $f$ measurable and $m \in \mathbb{R}$ , $\mu(\{|f - m| > t\}) = \mu(\{(f - m)^2 > t^2\})\leq t^{-2} \int (f - m)^2 \mathrm{d}\mu \\ P(|X - \mathbb{E}[X]| > t) \leq \frac{\text{Var}(X)}{t^2}$
Chernoff’s Inequality: For $f$ measurable and $m \in \mathbb{R}$ , $\mu(\{f > t\}) \leq e^{-tm} \int e^{mf} \mathrm{d}\mu \\$ In probability theory, the right hand side becomes the moment generating function or the Laplace transform.

Convex Functions on $\mathbb{R}$
Let $I \subset \mathbb{R}$ be an interval. A function $\phi : I \rightarrow \mathbb{R}$ is convex if for all $t \in [0, 1]$ and all $x, y \in I$ ,
$\phi(tx + (1 − t)y) \leq t\phi(x) + (1 − t)\phi(y)$

Jensen’s Inequality
Let $(\Omega, \mathcal{F}, P)$ be a probability space and $X$ an integrable random variable ( i.e. a measurable function in $L^1(\Omega, \mathcal{F}, P)~$ ) such that $X : \Omega \rightarrow I \subset \mathbb{R}$ . For any convex $\phi : I \rightarrow \mathbb{R}$ ,
$\phi(\int X \mathrm{d}P) \leq \int \phi(X) \mathrm{d}P$
which is $\phi(\mathbb{E}[X]) \leq \mathbb{E}[\phi(X)]$

Proof
For some $c \in I$ , if $X = c$ , $P$ -a.e., then the result is immediate. Otherwise, let $m = \mathbb{E}[X]$ be the mean of $X$ , which lies in the interior of interval. Then, we can choose $a, b \in \mathbb{R}$ such that $\phi(x) \geq ax + b$ for all $x \in I$ with equality at $x = m$ . Then, $\phi(X) \geq aX + b$ , and
$\phi(\mathbb{E}[X]) = am + b = \mathbb{E}[aX + b] \leq \mathbb{E}[\phi(X)]$
Lastly, to check that $\mathbb{E}[\phi(X)]$ is well defined (i.e. not $\infty−\infty$ ), we note that $\phi = \phi^+ −\phi^-$ where $\phi^-$ is concave and $\phi^-(x) \leq |a||x| + |b|$ . Hence, $\mathbb{E}[\phi(X)] \leq |a|\mathbb{E}|x| + |b| < \infty$ . $\square$

Hölder and Minkowski’s Inequalities#

Hölder’s Inequality
Let $p, q \in [1, \infty]$ be conjugate indices ( i.e. $\frac{1}{p} + \frac{1}{q} = 1$ ) and $f$ and $g$ be measurable, then $||fg||_1 \leq ||f||_p||g||_q$

Proof
If either $||f||_p = 0, \infty$ or $||g||_q = 0, \infty$ , then the result is immediate. Hence, for $f$ such that $0 < ||f||_p < \infty$ , we can normalize and without loss of generality assume that $||f||_p = 1$ . Then, we can define a probability measure $P$ on $\mathcal{F}$ such that for any $A \in \mathcal{F}$ ,
$P(A) \vcentcolon= \int_A f\mathrm{d}\mu$
Then, using Jensen’s Inequality with $\phi(x) = x^q$ and $q(p − 1) = p$ ,
$\begin{aligned} ||fg||_1 &= \int |fg| \mathrm{d}\mu = \int \frac{|g|}{|f|^{p - 1}}\mathbf{1}_{|f| > 0}\underbrace{|f|^p\mathrm{d}\mu}_{\color{#b984df}\text{prob measure }\mathrm{d}\nu} \\ &\leq \left[\int \left(\frac{|g|}{|f|^{p-1}}\mathbf{1}_{|f| > 0}\right)^q|f|^p\mathrm{d}\mu\right]^{\frac{1}{q}} \\ &\leq \left[\int |g|^q\mathrm{d}\mu\right]^\frac{1}{q} = ||f||_p||g||_q \end{aligned}$

From Hölder’s inequality with $p=q=2$ , we can derive Cauchy-Schwarz Inequality:

Cauchy-Schwarz Inequality
For measurable $f$ and $g$ , $||fg||_1\leq||f||_2||g||_2$

Minkowski’s Inequality
Let $p \in [1, \infty]$ and $f$ , $g$ be measurable functions, then $||f+g||_p\leq ||f||_p + ||g||_p$

Proof
If either $||f||_p = \infty$ or $||g||_p = \infty$ or $||f+g||_p=0$ , then we are done. If $p=1$ , then $|(f + g)(\omega)| \leq |f(\omega)| + |g(\omega)|$ and the result follows quickly. For $p\in (1, \infty]$ and $p, q$ conjugates, we note that
$|||f+g|^{p-1}||_q = \left[\int |f+g|^{(p-1)q}\mathrm{d}\mu\right]^\frac{1}{q} = \left[\int|f+g|^p\mathrm{d}\mu\right]^{\frac{p-1}{p}} = ||f + g||^{p-1}_p$
Then using the above equality, we have
$\begin{aligned} ||f+g||^p_p &= \int |f+g|^p\mathrm{d}\mu \leq \int |f||f+g|^{p-1}\mathrm{d}\mu + \int |g||f+g|^{p-1}\mathrm{d}\mu \\ &\leq ||f||_p|||f+g|^{p-1}||_q + ||g||_p|||f+g|^{p-1}||_q \\ &= (||f||_p + ||g||_p)||f+g||^{p-1}_p \end{aligned}$
Divide both sides by $||f + g||^{p−1}_p$ finishes the proof. $\square$

$L_p$ Approximation Theorem
Let $(\Omega, \mathcal{F}, \mu$ ) be a measure space, and let $\mathcal{A}$ be a $\pi$ -system such that $\sigma(A) = \mathcal{F}$ and $\mu(A) < \infty$ for all $A ∈ \mathcal{A}$ and there exists $A_i \uparrow \Omega, A_i \in \mathcal{A}$ . Let the collection of simple functions be
$V_0 \vcentcolon= \left\{\sum_{i=1}^n a_i\mathbf{1}_{A_i} : a_i \in \mathbb{R}, A_i\in\mathcal{A}, n\in\mathbb{N}\right\}$
For $p\in[1,\infty), V_0\subset L_p$ and for all $f\in L^p$ and all $\epsilon > 0$ , there exists a $v\in V_0$ such that $||f-v||_p < \epsilon$ .

Proof
For any $A \in \mathcal{A}, ||\mathbf{1}_A||_p = (\int\mathbf{1}_A\mathrm{d}\mu)^\frac{1}{p} = \mu(A)^\frac{1}{p} < \infty$ . Thus $\mathbf{1}_A\in L^p$ for all $A\in\mathcal{A}$ . Since $L^p$ is a linear space, $V_0 \subset L^p$ .
Next, let $V\subseteq L^p$ be all $\mathcal{F}\in L^p$ that can be approximated as above by some $v\in V_0$ and $\epsilon > 0$ . Let $f,g\in V$ be approximated by $v_f, v_g$ then by Minkowski’s Inequality,
$||f+g - (v_f + v_g)||_p \leq ||f - v_f||_p + ||g - v_g||_p < 2\epsilon$
Hence, $V$ is also a linear space.
Now, assume $\Omega\in\mathcal{A}$ ( i.e. $\mu(\Omega) < \infty$ ). Let $\mathcal{L} = \{B \in \Omega : \mathbf{1}_B\in V\}$ , which we will show is, in fact, a $\lambda$ -system. We know that $A \subset \mathcal{L}$ and thus $\Omega \in \mathcal{L}$ . For $A, B \in\mathcal{L}$ such that $A\subseteq B$ then $\mathbf{1}_{B\setminus A} = \mathbf{1}_B - \mathbf{1}_A \in V$ since $V$ is linear, so $B\setminus A\in\mathcal{L}$ . Lastly, for $\{A_i\}_{i=1}^\infty$ pairwise disjoint with $A_i \in \mathcal{L}$ , let $A = \bigcup_{i=1}^\infty A_i$ and $B_j = \bigcup_{i=1}^j A_i$ . Then, $B_j \uparrow A$ and $||\mathbf{1}_A − \mathbf{1}_{B_j}||_p = \mu(A \setminus B_j)^\frac{1}{p} \rightarrow 0$ . Therefore, $A \in \mathcal{L}$ , and thus $\mathcal{L}$ is a $\lambda$ -system. By Dynkin $\pi$ - $\lambda$ Theorem, $\mathcal{F}\subset\mathcal{L}$ and thus $\mathbf{1}_B\in V$ for any $B\in \mathcal{F}$ . Therefore, for any non-negative $f\in L^p$ , we can construct simple functions $f_n = \min\{n, 2^{-n}\lfloor 2^n\rfloor f\}$ such that $f_n\uparrow f$ . Then $|f - f_n|^p\rightarrow 0$ pointwise and $|f - f_n|^p \leq |f|^p$ . Hence, by Dominated Convergence Theorem, $||f - f_n||^p\rightarrow 0$ . Thus $f \in V$ and by the linearity of $V$ , $V = L^p$ .
Lastly, for general $\Omega$ , we have by assumption a sequence $A_i \uparrow \Omega$ . Hence, for any $f \in L^p$ , we have that $f\mathbf{1}_{A_i} \in V$ and similarly to above, $|f − f\mathbf{1}_{A_i}|^p \rightarrow 0$ pointwise and $|f − f\mathbf{1}_{A_i}|^p \leq |f|^p$ . Therefore, $||f − f\mathbf{1}_{A_i}||_p \rightarrow 0$ by dominiated convergence. Thus, $f \in V$ . $\square$

Convergence in Probability & Measure#

Convergence of Measure#

Weak Convergence of Measure
Let $S$ be a metric space and $\mathcal{S}$ be the Borel $\sigma$ -Field on $S$ . Then, for a measure $P$ and a sequence $\{P_i\}_{i=1}^\infty$ , we say that $P_i$ converges weakly to $P$ , i.e. $P_i \Rightarrow P$ , if
$\int f \mathrm{d}P_i \rightarrow \int f \mathrm{d}P$
for all $f\in \mathscr{C}^0_B(\mathbb{R})$ , all continuous bounded real-valued functions on $S$ .

Portmanteau Theorem
For $P$ and $P_i$ on a metric space $(S, \mathcal{S})$ , the following are equivalent:
$P_i \Rightarrow P$
$\int f\mathrm{d}P_i\rightarrow\int f\mathrm{d}P$ for all bounded uniformly continuous functions $f$
$\limsup_i P_i(C) \leq P(C)$ for all closed sets $C$
$\liminf_i P_i(U) \geq P(U)$ for all open sets $U$
$\lim_i P_i(A) = P(A)$ for all sets $A\in\mathcal{S}$ with $P(\partial A) = 0$

Proof
(1) $\rightarrow$ (2) If convergence holds for every $f \in \mathscr{C}^0_B$ then is certainly hold for all bounded uniformly continous $f$ .
(2) $\rightarrow$ (3) For any $C$ closed and $\epsilon > 0$ there exists a $\delta > 0$ such that for $C_δ = \{x \in S : d(x, C) < \delta\}$ , we have $P(C_\delta) < P(C) + \epsilon$ as $C_\delta \downarrow C$ as $\delta\rightarrow 0^+$ . Then, we can define an $f$ such that $f = 1$ on $C$ , $f = 0$ on $S \setminus C_\delta$ . Then $f$ is uniformly continuous (by Urysohn’s Lemma) and $0 \leq f \leq 1$ Then, by (2), we have that
$P_i(C) \leq \int f\mathrm{d}P_i\rightarrow\int f\mathrm{d}P \leq P(C_\delta) < P(C) + \epsilon$
Thus, taking the $\limsup$ and $\epsilon$ to zero gives $\limsup_i P_i(C) \leq P(C)$
(3) $\rightarrow$ (1) Let $f \in \mathscr{C}^0_B(\mathbb{R})$ . Our goal is to show that $\limsup_i\int f \mathrm{d}P_i \leq\int f \mathrm{d}P$ and similarly for $\liminf$ to show (1) holds. As $f$ is bounded, we can shift and scale it, and without loss of generality, we assume that $0 < f < 1$ . Then, for any choice of $n \in \mathbb{N}$ , we define nested closed sets $C_j = \{x\in S : f(x)\geq j/n\}$ for all $j= 1, 2, \ldots, n$ and cut $f$ into pieces to get
$\sum_{j=1}^n\frac{j-1}{n}P(C_{j-1}\setminus C_j) \leq \int f\mathrm{d}P \leq \sum_{j=1}^n\frac{j}{n}P(C_{j-1}\setminus C_j)$
Also, $P(C_{j-1}\setminus C_j) = P(C_{j-1}) - P(C_j)$ , the above becomes
$\frac{1}{n}\sum_{j=1}^n P(C_j) \leq \int f\mathrm{d}P \leq \frac{1}{n} + \frac{1}{n}\sum_{j=1}^n P(C_{j})$
Thus,
$\limsup_i \int f\mathrm{d}P_i \leq \frac{1}{n} + \frac{1}{n}\sum_{j=1}^n \limsup_i P_i(C_j) \leq \frac{1}{n} + \frac{1}{n}\sum_{j=1}^n P(C_j) \leq \frac{1}{n} + \int f\mathrm{d}P$
Taking $n \rightarrow \infty$ gives $\limsup_i \int f \mathrm{d}P_i \leq \int f \mathrm{d}P$ . Replacing $f$ with $−f$ gives $\liminf_i f \mathrm{d}P_i \geq \int f \mathrm{d}P$ . Thus the $\limsup$ and $\liminf$ coincide proving that (3) $\rightarrow$ (1).
(3) $\Leftrightarrow$ (4) Let $U$ be the complement of $C$ . Then, $P(U) = 1 - P(C)$ Thus, $\limsup_i P_i(C) \leq P(C)$ is equivalent to $\liminf_i P_i(U) \geq P(U)$ .
(3)(4) $\Leftrightarrow$ (5) For any set $A\in\mathcal{S}$ with $P(\partial A) = 0$ , $A^\circ$ is an open set and $\bar{A}$ is a closed set. If (3) and (4) hold, we have that
$P(A^\circ) \leq \liminf_i P_i(A^\circ) \leq \liminf_i P_i(A) \leq \limsup_i P_i(\bar{A}) \leq \limsup_i P_i(\bar{A}) \leq P(\bar{A})$
Since $P(\partial A)=0$ , we have that $P(A^\circ) = P(\bar{A})$ . This is equivalent to $\lim_i P_i(A) = P(A)$ , which is (5). $\square$

Convergence of Random Variables#

In contrast to convergence of measures, let $(\Omega, \mathcal{F}, \mu)$ be a probability space and $(S, \mathcal{S})$ be a metric space with Borel sets as above. Then, for a random variable (i.e. measurable function) $X : \Omega → S$ , we can define a probability measure

P(A) \vcentcolon= \mu(X^{-1}(A)) ~~~ A\in\mathcal{S}

This is the distribution of $X$ . Then the expectation of a random variable can be written in multiple ways due to change of variables:

E[X] = \int_\Omega X(\omega) \mathrm{d}\mu(\omega) = \int_S x \mathrm{d}P(x)

Note that above Portmanteau Theorem can be rephrased for random variables as well.

Convergence in Distribution
For a sequence of random variables $\{X_i\}_{i=1}^\infty$ , we say that $X_i$ converges to $X$ in distribution ( denoted $X_i\overset{d}{\longrightarrow}X$ ) if $P_i \Rightarrow P$ .

Convergence in Probability
For a sequence of random variables $\{X_i\}_{i=1}^\infty$ , we say that $X_i$ converges to $X$ in probabilty ( denoted $X_i\overset{P}{\longrightarrow}X$ ) if for all $\epsilon > 0$
$\mu(\{\omega \in \Omega : d(X_i(\omega), X(\omega)) > \epsilon\}) \rightarrow 0$
In short, $P(d(X_i, X)>\epsilon)\rightarrow 0$ .

This means that the measure of the set of $\omega$ where $X_i(\omega)$ and $X(\omega)$ differ by more than $\epsilon$ goes to zero as $i \rightarrow \infty$ . Convergence in probability is closely connected to the metric $d$ on $(S, \mathcal{S})$ .

Convergence Almost Surely
For a sequence of random variables $\{X_i\}_{i=1}^\infty$ , we say that $X_i$ converges almost surely to $X$ ( denoted $X_i\overset{\text{a.s.}}{\longrightarrow}X$ ) if
$\mu(\{\omega \in \Omega : X_i(\omega) \rightarrow X(\omega)\}) = 1$
i.e. pointwise convergence almost everywhere.

Convergence in $L^p$
For a sequence of random variables $\{X_i\}_{i=1}^\infty$ , we say that $X_i$ converges to $X$ in $L^p$ if
$E[d(X_i - X)^p] = \int d(X_i(\omega), X(\omega))^p\mathrm{d}\mu(\omega) \rightarrow 0$

Here, we can think of $d(X_i(\omega), X(\omega))$ as a function from $\Omega$ to $\mathbb{R}^+$ . In the case that we have real valued random variables, i.e. $S = \mathbb{R}$ , then this is

\int |X_i - X|^p\mathrm{d}\mu \rightarrow 0

Hierarchy of Convergence Types#

Conv a.s. $\Rightarrow$ conv in probability
Conv in probability $\Rightarrow$ conv in distribution
For $1\leq p < q \leq \infty$ , conv in $L^p$ $\Rightarrow$ conv in $L^q$
For any $p\in [1, \infty]$ , conv in $L^p$ $\Rightarrow$ conv in probability

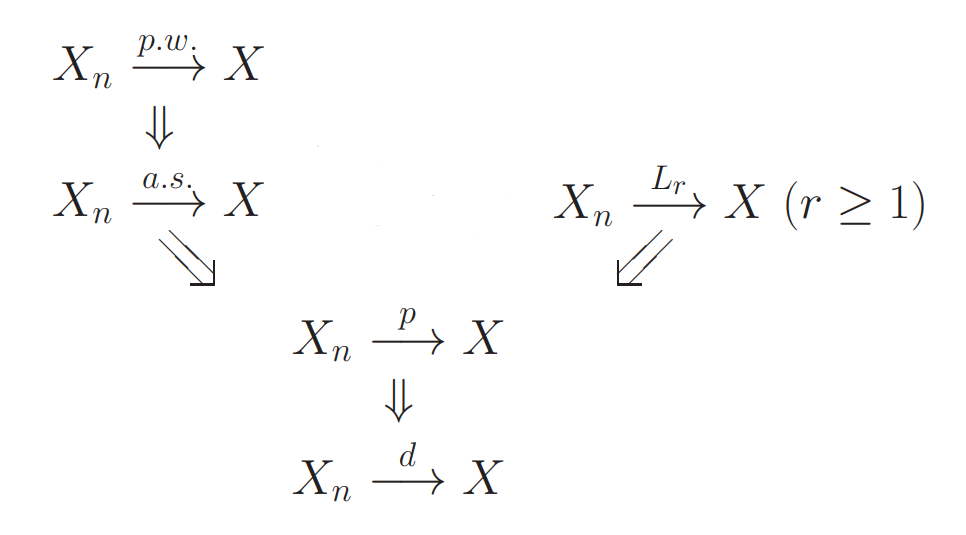
Borel-Cantelli Lemmas#

Let $(\Omega, \mathcal{F}, \mu)$ be a probability space. For $\{A_i\}_{i=1}^\infty, A_i\in \mathcal{F}$ , then we define

\limsup_i A_i = \bigcap_{i=1}^\infty\bigcup_{j > i} A_j ~~~\text{and}~~~ \liminf_i A_i = \bigcup_{i=1}^\infty\bigcap_{j > i} A_j

The set $\limsup_i A_i$ is sometimes referred to as $A_i$ infinitely often or $A_i$ i.o. This is because $\omega \in \limsup_i A_i$ implies that for any $N \in \mathbb{N}$ there exists an $n > N$ such that $\omega\in A_n$ . Similarly, some write $A_i$ eventually or $A_i$ ev. for $\liminf_i A_i$ . This is because for $\omega \in \liminf_i A_i$ then there exists an $N$ large enough such that $\omega \in A_n$ for all $n \geq N$ .

1st Borel-Cantelli Lemma
Let $\{A_i\}_{i=1}^\infty$ with $A_i \in \mathcal{F}$ . If $\sum_{i=1}^\infty \mu(A_i) < \infty$ , then $\mu(\limsup_i A_i) = 0$ .

Proof
As the summation converges, then the tail sum has to tend to zero, we have simply that
$\mu(\limsup_i A_i) = \mu\left(\bigcap_{i=1}^\infty\bigcup_{j > i} A_j\right) \leq \mu\left(\bigcup_{j > i} A_j\right) \leq \sum_{j > i} \mu(A_j) \rightarrow 0$
as $i\rightarrow \infty$ . $\square$

2nd Borel-Cantelli Lemma
Let $\{A_i\}_{i=1}^\infty$ be an independent collection with $A_i \in \mathcal{F}$ . If $\sum_{i=1}^\infty \mu(A_i) = \infty$ , then $\mu(\limsup_i A_i) = 1$ .

Proof
Note that $1 − t \leq e^{−t}$ for all $t \in \mathbb{R}$ and we have that the independence of the $\{A_i\}_{i=1}^\infty$ implies the independence $\{A^c_i\}_{i=1}^\infty$ . Therefore, for any $i \in \mathbb{N}$ and $k \geq i$ ,
$\mu(\bigcap_{j=i}^k A^c_j) = \prod_{j=i}^k (1 - \mu(A_j)) \leq \exp\left(-\sum_{j=i}^k \mu(A_j)\right)$
Taking $k \rightarrow \infty$ takes the right hand side to zero. Hence, $\mu(\cap_{j>i} A^c_j) = 0$ for all $i$ . Thus,
$\mu(\limsup_i A_i) = \mu\left(\bigcap_{i=1}^\infty\bigcup_{j > i} A_j\right) = 1 - \mu\left(\bigcup_{i=1}^\infty \bigcap _{j > i} A^c_j\right) = 1$
which is the desired result. $\square$

Law of Large Numbers#

Let $\{X_i\}_{i=1}^\infty$ be random variables from $(\Omega, \mathcal{F}, P)$ to $(\mathbb{R}, \mathcal{B})$ . Hence, for any $A \in \mathcal{B}$ , we write

P(X \in A)\vcentcolon= P(\{\omega \in \Omega : X(\omega) \in A\}).

and $E[X] = \int X(\omega)\mathrm{d}P$ . Furthermore, we define the partial sum $S_n = \sum^n_{i=1} X_i$ , which is also a measurable random variable.

Independence
For random variables $X$ and $Y$ on the same probability space $(\Omega, \mathcal{F}, P)$ but possibly with different codomains, $(\mathbb{X}, \mathcal{X})$ and $(Y, \mathcal{Y})$ respectively, we say that $X$ and $Y$ are independent if
$P(\{X \in A\}\cap \{Y \in B\}) = P(X \in A)P(Y \in B)$
for all $A \in \mathcal{X}$ and $B \in \mathcal{Y}$ .

This definition can be extended to a finite collection of random variables $\{X_i\}^n_{i=1}$ implying

P(\bigcap_{i=1}^n \{X_i \in A_i\}) = \prod^n_{i=1} P(X_i \in A_i)

for all $A_i$ . We say that an infinite collection of random variables is independent if all finite collections are independent.

Note that since $\{X \in A\}$ is shorthand for $\{\omega \in \Omega : X(\omega) \in A\} = X^{−1}(A)$ , random variables $X$ and $Y$ are independent if and only if the $\sigma$ -fields $\sigma(X)$ and $\sigma(Y)$ are independent ( defined in here ).

Identically Distributed
For $X : \Omega → \mathbb{R}$ , the distribution of $X$ is the measure induced by $X$ on $\mathbb{R}$ , i.e., $P\circ X^{-1}(A)$ for $A\in \mathcal{B}$ . We say that $X$ and $Y$ are identically distributed if $P \circ X^{−1}$ and $P \circ Y^{-1}$ coincide almost surely.

Weak Law of Large Numbers#

Weak Law of Large Numbers
Let $(\Omega, \mathcal{F}, P)$ be a probability space and $\{X_i\}_{i=1}^\infty$ be random variables (measurable functions) from $\Omega$ to $\mathbb{R}$ such that $E[X_i] = c \in \mathbb{R}$ and $E[X_i^2]=1$ for all $i$ and $E[(X_i − c)(X_j − c)] = 0$ for all $i \neq j$ . Then $\frac{S_n}{n} \overset{P}{\longrightarrow} c$ .

Proof
Without loss of generality, we assume $c = 0$ . Otherwise, we can replace $X_i$ with $X_i − c$ . Then, for any $t > 0$ , Chebyshev’s inequality implies that
$P(\frac{|S_n|}{n} \geq t) \leq \frac{E[S_n^2]}{n^2t^2} = \frac{1}{n^2t^2}E[(\sum^n_{i=1} X_i)^2] = \frac{1}{n^2t^2}E[\sum^n_{i=1} X_i^2] = \frac{1}{nt^2} \to 0$
as $n \to \infty$ . $\square$

Note that in the above proof, we only require that the $X_i$ be uncorrelated (i.e. $E[(X_i −c)(X_j −c)] = 0$ ) and not independent. In the next theorem, we require independence, but remove all second moment conditions.

Strong Law of Large Numbers#

Strong Law of Large Numbers
Let $\{X_i\}_{i=1}^\infty$ be i.i.d. random variables from $\Omega$ to $\mathbb{R}$ .
If $E[|X_i|] = \infty$ , then $\frac{S_n}{n}$ does not converge to any finite value.
If $E[|X_i|] < \infty$ , then $\frac{S_n}{n} \overset{a.s.}{\longrightarrow} c$ for $c = E[X_i]$ .

Proof
Assume that $\frac{S_n}{n} \longrightarrow c \in \mathbb{R}$ but also that $E[|X_i|] = \infty$ , and note that $\frac{X_n}{n} = \frac{S_n − S_{n−1}}{n} \to 0$ . Since $E[|X_i|] = \infty$ , then $\sum_{n=0}^\infty P(X_i > n) = \infty$ and 2nd Borel-Cantelli Lemma says that $|X_n| > n$ for infinitely many $n$ . Thus
$P(\{\omega\in\Omega : \frac{S_n - S_{n-1}}{n}\to 0\}) = 0$
Thus $\frac{S_n}{n}\nrightarrow c \in \mathbb{R}$ .
Assume that $E[X_i] = c \in \mathbb{R}$ . Without loss of generality, we assume $X_i \geq 0$ for all $i$ . Otherwise, we can write $X = X^+ − X^−$ and independence of $X$ and $Y$ implies independence for $X^+$ and $Y^+$ . Also, we use $F$ to denote the distribution of $X$ , i.e. $F(x) = P(X \leq x)$ .
We define $Y_i = X_i\mathbf{1}_{X_i\leq i}$ and $T_n = \sum_{i=1}^n Y_i$ . For any $\delta > 1$ , we can define a non-decreasing integer sequence $k_n = \lfloor \delta^n \rfloor$ . Then $1\leq k_n\leq \delta^n < k_n + 1 \leq 2k_n$ and $k_n^{-2}\leq 4\delta^{-2n}$ . Therefore,
$\sum_{n=1}^\infty k_n^{-2}\mathbf{1}_{k_n \geq i}\leq 4\sum_{n = 1}^\infty \delta^{-2n}\mathbf{1}_{\delta^n\geq i} = \frac{4}{i^2(1 - \delta^{-2})}\leq c_0 i^{-2} \tag{1}$
for some constant $c_0$ . We also note that $\sum_{i=k+1}^\infty i^{−2} < \int_k^\infty x^{-2}\mathrm{d}x = \frac{1}{k}$ . By Chebyshev’s inequality, $\forall t > 0$ , $\exists~ c_1$ depending on $t$ and $\delta$ such that
$\begin{aligned} \sum_{n=1}^\infty P(|T_{k_n} - E[T_{k_n}]| \geq tk_n) &\leq c_1\sum_{n=1}^\infty k_n^{-2}\text{Var}(T_{k_n}) \\ &= c_1\sum_{n=1}^\infty k_n^{-2}\sum_{i=1}^{k_n}\text{Var}(Y_i) \\ &\leq c_1\sum_{n=1}^\infty \text{Var}(Y_i)\sum_{k_n\geq i}k_n^{-2} \\ &\leq c_2\sum_{n=1}^\infty i^{-2}\text{Var}(Y_i) ~~~\text{by (1)}\\ &= c_2\sum_{i=1}^\infty i^{-2}\int_0^i x^2\mathrm{d}F(x) \\ &= c_2\sum_{i=1}^\infty i^{-2}\left\{\sum_{k=0}^{i-1}\int_k^{k+1}x^2\mathrm{d}F(x)\right\} \\ &\leq c_3\sum_{k=0}^\infty \frac{1}{k+1}\int_k^{k+1}x^2\mathrm{d}F(x) \\ &\leq c_3\sum_{k=0}^\infty \int_k^{k+1}x\mathrm{d}F(x) = c_3E[X_i] < \infty \end{aligned}$
And thus $\sum_{n=1}^\infty P(|T_{k_n} - E[T_{k_n}]| \geq tk_n) < \infty$ . Hence, by 1st Borel-Cantelli Lemma, $n^{-1}(|T_{k_n} - E[T_{k_n}])\overset{a.s.}\longrightarrow0$ . Since $E[Y_n]\uparrow E[X_i]$ , we have that ${k_n}^{-1}E[T_{k_n}]\uparrow E[X_i]$ and in turn that $n^{-1}T_{k_n}\overset{a.s.}\longrightarrow E[X_i]$ .
To get back to $X_i$ and $S_n$ , we note that $E[X] <\infty$ if and only if $\sum_{i=0}^\infty P (X > i) < \infty$ . Thus $\sum_{i=1}^\infty P (X_i \neq Y_i) = \sum_{i=1}^\infty P (X_i > i) < \infty$ and 21stnd Borel-Cantelli Lemma says that $P (\limsup\{X_i \neq Y_i\}) = 0$ so for $i$ large enough, $X_i = Y_i$ a.s. We define “large enough” to be $i > m(\omega)$ ( i.e. $X_i(\omega) = Y_i(\omega) ~~ \forall i > m(\omega)$ ) Furthermore, $k_n^{−1} S_{m(\omega)} \to 0$ and $k_n^{−1}T_{m(\omega)} \to 0$ as $n \to \infty$ , meaning that the contribution of the terms where $X_i$ and $Y_i$ may not coincide becomes negligible. Hence, $k_n^{-1}S_{k_n}\overset{a.s.}\longrightarrow E[X_i]$ , so we have almost sure convergence of a subsequence.
Finally, since $k_{n+1}/k_n \to \delta$ , there exists an $n$ large enough such that $1 \leq k_{n+1}/k_n < \delta^2$ . Thus, for $k_n < i < k_{n+1}$ ,
$k_n^{-1}S_{k_n}\leq \delta^2\frac{S_i}{i}\leq \delta^4 k_{n+1}^{-1}S_{k_{n+1}} \\ \delta^{-2}E[X_i] \leq \limsup_{n\to\infty}\frac{S_i}{i} \leq \limsup_{i\to\infty}\frac{S_i}{i} \leq \delta^2 E[X_i]$
Thus, taking $\delta\to 1$ concludes the proof. $\square$

Central Limit Theorem#

Gaussian Measure on $\mathbb{R}$
A Borel measure $\gamma$ on $(\mathbb{R}, \mathcal{B})$ is said to be Gaussian with mean $m$ and variance $\sigma$ if
$\gamma((a, b]) = \frac{1}{\sigma\sqrt{2\pi}}\int_a^b e^{-(x-m)^2/2\sigma^2}\mathrm{d}\lambda(x)$

Gaussian Measure on $\mathbb{R}^d$
A Borel measure $\gamma$ on $(\mathbb{R}^d, \mathcal{B})$ is said to be Gaussian if for all linear functionals $f : \mathbb{R}^d \rightarrow \mathbb{R}$ , the induced measure $\gamma \circ f^{−1}$ on $(\mathbb{R}, \mathcal{B})$ is Gaussian.

Gaussian Random Variable
A random variable $Z$ from a probability space $(\Omega, \mathcal{F}, \mu)$ to $(\mathbb{R}^d, \mathcal{B})$ is said to be Gaussian if $\gamma \vcentcolon= \mu \circ Z^{−1}$ is a Gaussian measure on $(\mathbb{R}^d, \mathcal{B})$ .

Characteristic Function
For a probability measure $\mu$ on $(\mathbb{R}^d, \mathcal{B})$ , the characteristic function (Fourier transform) $\tilde{\mu}$ : \mathbb{R}^d \rightarrow \mathbb{C}$ is defined as
$\tilde{\mu}(t) \vcentcolon= \int \exp\{i\langle x, t\rangle\}\mathrm{d}\mu(x)$
We can also invert the above transformation. That is, if $\tilde{\mu}$ is integrable with respect to Lebesgue measure on $\mathbb{R}^d$ , then
$p(x) = (2\pi)^{-d}\int \tilde{\mu}(t)\exp\{-i\langle x, t\rangle\}\mathrm{d}\lambda(t)~~~\lambda-a.e.$

Convolution
For two measures $\mu$ and $\nu$ on $(\mathbb{R}^d, \mathcal{B})$ , the convolution measure is defined as
$(\mu * \nu)(B) \vcentcolon= \int \nu(B − x)\mathrm{d}\mu(x)$
for all $B \in \mathcal{B}$ where $B - x = \{y \in \mathbb{R}^d : y +x \in B\}$ .

Note that the convolution operator $*$ is commutative and associative. Also, for two independent random variables $X$ and $Y$ with corresponding measures $\mu$ and $\nu$ , the measure of $X + Y$ is $\mu * \nu$ .

Uniquesness of Characteristic Function Theorem
Let $\mu$ and $\nu$ be probability measures on $(\mathbb{R}^d, \mathcal{B})$ . If $\tilde{\mu} = \tilde{\nu}$ then $\mu = \nu$ .

Proof
Let $\gamma_\sigma$ be a mean zero Gaussian measure on $\mathbb{R}^d$ with variance $\sigma^2I$ . We denote $\mu^{(\sigma)} = \mu * \gamma_\sigma$ and similarly for $\nu^{(\sigma)}$ . It can be shown that the corresponding density functions for $\mu^{(\sigma)}$ and $\nu^{(\sigma)}$ are
$p^{(\sigma)}(x) = \frac{1}{(2\pi)^d}\int \tilde{\mu}(t)\exp\left\{-i\langle x, t\rangle - \frac{1}{2}\sigma^2|t|^2\right\}\mathrm{d}\lambda(t) \\ q^{(\sigma)}(x) = \frac{1}{(2\pi)^d}\int \tilde{\nu}(t)\exp\left\{-i\langle x, t\rangle - \frac{1}{2}\sigma^2|t|^2\right\}\mathrm{d}\lambda(t)$
Since $\tilde{\mu} = \tilde{\nu}$ , we have that $p^{(\sigma)} = q^{(\sigma)}$ for all $\sigma > 0$ .
Let $X$ be a random variable corresponding to $\mu$ and $Z$ to $\gamma_1$ . Then, the measure $\mu^{(\sigma)}$ is paired with the random variable $X + \sigma Z$ . Thus $X+\sigma Z\overset{a.s.}{\longrightarrow}X$ as $\sigma\downarrow 0$ , that is, pointwise for almost all $\omega$ . Thus, this convergence holds in probability and thus in distribution, i.e $\mu^{(\sigma)}\Rightarrow\mu$ as $\sigma\downarrow 0$ .
Lastly, we have that $\mu^{(\sigma)} \Rightarrow \mu$ and $\nu^{(\sigma)} \Rightarrow \nu$ . Since the limit is unique $\mu = \nu$ . $\square$

Central Limit Theorem
Let $(\Omega, \mathcal{F}, P)$ be a probability space, $\{X_i\}_{i=1}^\infty$ be i.i.d. random variables on $(\mathbb{R}^d, \mathcal{B})$ such that $E[X_i] = 0$ and $E[|X_i|^2] < \infty$ . Let $S_n = \sum_{j=1}^n X_j$ . Then, $n^{-1/2}S_n\overset{d}{\longrightarrow}Z$ where $Z$ is a gaussian random variable with zero mean and covariance $\Sigma$ with $jk$ th entry $\Sigma_{jk} = E[X_{ij}X_{ik}]$ .

Proof
As the random vectors $X_i$ are mean zero and independent $E[\langle X_j, X_k \rangle] = 0$ for $j\neq k$ . In turn, for any $n$ ,
$E\left[|n^{-1/2}S_n|^2\right] = n^{-1}E\left[\sum_{j,k=1}^n\langle X_j, X_k \rangle\right] = E\left[|X_j|^2\right]$
For any $\epsilon > 0$ , there exists an $M_\epsilon > 0$ such that $E[|X_j|^2]/M_\epsilon^2 < ε$ . Thus, from Chebyshev’s inequality, we have that $P(|n^{−1/2}S_n| > M_\epsilon) < \epsilon$ . This implies that the sequence $n^{−1/2}S_n$ is “uniformly tight.
For a vector $v \in \mathbb{R}^d$ , the random variables $\langle X_j, v \rangle$ are i.i.d. real-valued with $E[\langle X_j, v\rangle] = 0$ and $E[\langle X_j, v\rangle^2] < \infty$ . Let $h(v) \vcentcolon= E[\exp(i\langle X_j, v\rangle)]$ be the characteristic function of $X_j$ .Then, $h(0) = 1$ and $\nabla h(0)=0$ and $\nabla^2 h(0) = -\Sigma$ Thus, by Taylor’s Theorem, we have
$h(v) = 1 - \frac{1}{2}v^\mathrm{T}\Sigma v + o(||v||_2^2)$
Thus, for any fixed vector $v$ ,
$E\left[\exp\left\{i\langle n^{-1/2}S_n, v\rangle \right\}\right] = h(n^{-1/2}v)^n = \left[1 - \frac{v^\mathrm{T}\Sigma v}{2n} + o\left(\frac{||v||_2^2}{n}\right)\right]^n \to \exp\left\{-\frac{1}{2}v^\mathrm{T}\Sigma v\right\}$
as $n\to\infty$ . Thus, by the Uniqueness of Characteristic Function Theorem, we have that $n^{−1/2}S_n\overset{d}{\longrightarrow}Z$ where $Z$ is a Gaussian random variable with zero mean and covariance $\Sigma$ . $\square$

Erogodic Theorem#

Measure Preserving Map
Let $(\Omega, \mathcal{F}, \mu)$ be a measure space. A mapping $T : \Omega \to \Omega$ is called measure preserving if
$\mu(T^{-1}(A)) = \mu(A)~~~ \forall A\in \mathcal{F}$
Invariant Set and Function
For a mapping $T : \Omega\to\Omega$ ,
A set $A \in \mathcal{F}$ is $T$ -invariant if $T^{−1}(A) = A$ . The set of all $T$ -invariant sets forms a $\sigma$ -field $\mathcal{F}_T$ .
A measurable function $f : \Omega\to\mathbb{R}$ is $T$ -invariant if $f = f \circ T$ . $f$ is $T$ -invariant if and only if $f$ is $\mathcal{F}_T$ -measurable, i.e. $\forall B \in\mathcal{B}(\mathbb{R}), f^{-1}(B)\in \mathcal{F}_T$

Ergodic Map
A mapping $T$ is said to be ergodic if for any $A \in \mathcal{F}_T$ ,
$\mu(A) = 0 ~~~\text{or}~~~ \mu(A^c) = 0$

Example

For Lebesgue measure on $(0, 1]$ , two examples of measure preserving maps are the shift map

T(x) = x + a \mod 1

and Baker’s Map

T(x) = 2x - \lfloor 2x \rfloor

Furthermore, it can be shown that

If $f$ is integrable and $T$ is measure preserving then $f \circ T$ is integrable and

\int f\mathrm{d}\mu = \int f\circ T\mathrm{d}\mu

If $T$ is ergodic and $f$ is invariant, then $f = c~$ $µ$ -a.e. for some constant $c$ .

Birkhoff and von Neumann’s Theorems#

In what follows, we let $(\Omega, \mathcal{F}, \mu)$ be a measure space, $T$ be a measure preserving transformation, $f : \Omega \rightarrow\mathbb{R}$ a measurable function, and

S_n = S_n(f) = f + f \circ T + \cdots + f \circ T^{n−1}

where $S_0 = 0$ .

Maximal Ergodic Lemma
Let $f$ be integrable and $S^∗$ = $\sup_{n\geq 0} S_n(f)$ (element-wise maximum). Then,
$\int_{S^∗ > 0} f \mathrm{d}\mu \geq 0$

Proof
Let $S^∗_n = \max_{0\leq m\leq n} S_m(f)$ and $A_n = \{\omega \in \Omega : S^∗_n(ω) > 0\}$ . Then, for $1 \leq m \leq n$ ,
$S_m = f + S_{m - 1}\circ T \leq f + S^*_n \circ T$
Furthermore, on the set $A_n$ ,
$S_n^* = \max_{0\leq m\leq n} S_m(f) \leq f + S^*_n \circ T$
On the set $A_n^c$ , $S^∗_n = 0$ since $S_0=0$ and we have that $S^∗_n = 0 \leq S^∗_n \circ T$ Thus, integrating both sides of the above gives
$\int_{\Omega} S^∗_n \mathrm{d}\mu \leq \int_{A_n} f \mathrm{d}\mu + \int_{A_n} S^∗_n \circ T \mathrm{d}\mu$
Since $S^∗_n$ is integrable and $T$ is measure preserving, $\int S^∗_n\mathrm{d}\mu = \int S^*n \circ T \mathrm{d}\mu < \infty$ . Thus, we have $\int_{A_n} f\mathrm{d}\mu \geq 0$ . As $n \rightarrow \infty, A_n\uparrow \{S_n^* > 0\}$ , we have that
$\int_S{n^* > 0} f \mathrm{d}\mu \geq 0 = \lim_{n \rightarrow 0}\int_{A_n} f \mathrm{d}\mu \geq 0$
due to Dominated Convergencee Theorem with $|f|$ as the dominating function. $\square$

Birkhoff’s Ergodic Theorem
Let $(\Omega, \mathcal{F}, \mu)$ be a $\sigma$ -finite measure space and $f \in L^1(\Omega, \mathcal{F}, \mu)$ . Then, there exists an $T$ -invariant $\bar{f} \in L(\Omega, \mathcal{F}, \mu)$ such that
$\int |\bar{f}| \mathrm{d}\mu \leq \int |f| \mathrm{d}\mu$
and $n^{−1}S_n(f) \rightarrow \bar{f}$ as $n \rightarrow \infty$ $\mu$ -a.e.

Proof
Both $\liminf_{n\rightarrow \infty}n^{-1}S_n(f)$ and $\limsup_{n\rightarrow \infty} n^{−1}S_n(f)$ are $T$ -invariant. Indeed, $n^{-1}S_n(f)\circ T = n^{-1}[S_{n + 1}(f) - f] = [(n + 1) / n](n + 1)^{-1}S_{n + 1}(f) - n^{-1}f$ Thus, we can define a set for $a < b$
$D_{a, b} = \left\{\omega\in\Omega : \liminf_{n\rightarrow\infty}\frac{S_n(f)(\omega)}{n} < a < b < \limsup_{n\rightarrow\infty}\frac{S_n(f)(\omega)}{n}\right\}$
which means that the $\liminf$ and $\limsup$ are separated, and this set $D_{a,b}$ is $T$ -invariant. The goal of the proof is to show that $\mu(D_{a,b}) = 0$ . Without loss of generality, we take $b > 0$ . Otherwise, $a < 0$ and we multiply everything by $-1$ .
For some $B \in F$ such that $\mu(B) < \infty$ , then we set $g = f − b\mathbf{1}B$ . Function $g$ is integrable and for each $x \in D_{a,b}$ , there is an $n$ such that $S_n(g)(x) \geq S_n(f)(x) − nb \geq 0$ since $b < \limsup_{n\rightarrow 0} n^{−1}S_n(f)$ . Thus, $S^∗(g) > 0$ and the Maximal Ergodic Lemma says that
$0\leq\int_D (f - b\mathbf{1}_B)\mathrm{d}\mu = \int_D f\mathrm{d}\mu - b\mu(B)$
As $\mu$ is $\sigma$ -finite, there exist such a sequence of sets $B_n \in F$ such that $B_n \uparrow D_{a,b}$ and $\mu(B_n) < \infty$ for all $n$ . Thus,
$b\mu(D_{a, b}) = \lim_{n\rightarrow\infty}b\mu(B_n) \leq \int_{D_{a, b}} f\mathrm{d}\mu$
This implies that $\mu(D_{a,b}) < \infty$ . Redoing the above argument for $−a$ and $−f$ results in $-a\mu(D_{a,b})\leq \int_{D_{a,b}}(-f)\mathrm{d}\mu$ . Therefore,
$b\mu(D_{a,b}) \leq \int_{D_{a,b}} f\mathrm{d}\mu \leq -a\mu(D_{a,b})$
and since $a < b$ , we have that $\mu(D_{a,b}) = 0$ .
Next, let
$E = \{\omega\in\Omega : \liminf_{n\rightarrow\infty}n^{-1}S_n(f)\} < \limsup_{n\rightarrow \infty}n^{-1}S_n(f)$
Then, $E$ is $T$ -invariant as the $\liminf$ and $\limsup$ are. Furthermore, $E = \bigcup_{a,b}\in\{a, b\in\mathbb{Q},a<b, D_{a,b}\}$ . Thus, $\mu(E) = 0$ .
This means that $n^{−1}S_n(f)$ converges in $[-\infty, \infty]$ on $E^c$ . Therefore, we define
$\bar{f} = \begin{cases} \lim_{n\rightarrow\infty}n^{-1}S_n(f) &~ \omega\in E^c \\ -\infty &~ \omega\in E \end{cases}$
Lastly, $\int f\circ T^n \mathrm{d}\mu = \int f \mathrm{d}\mu$ ( $T$ is measure preserving )and thus $\int |S_n(f)|\mathrm{d}\mu \leq n \int |f|\mathrm{d}\mu$ for all $n$ . Applying Fatou’s Lemma gives
$\int |\bar{f}|\mathrm{d}\mu = \int \lim_{n\to\infty}|n^{-1}S_n(f)|\mathrm{d}\mu \leq \liminf_{n\rightarrow\infty}\int |n^{-1}S_n(f)|\mathrm{d}\mu \leq \int |f|\mathrm{d}\mu$
finishing the proof. $\square$

Von Neumann’s Ergodic Theorem
Let $\mu(\Omega) < \infty$ and $p \in [1, \infty)$ . Then, for all $f \in L^p(\Omega, \mathcal{F}, \mu)$ , there exists an $\bar{f} \in L^p$ such that $n^{-1}S_n(f) \overset{L^p}{\longrightarrow} \bar{f}$ and
$\int \bar{f} \mathrm{d}\mu = \int f \mathrm{d}\mu$

Proof

We begin by noting that

||f\circ T^n||^p_p = \int |f|^p\circ T^n\mathrm{d}\mu = ||f||^p_p

By the above and the Minkowski’s Inequality, $||n^{-1}S_n(f)||_p \leq ||f||_p$ . Since $f\in L^p$ , given a $\epsilon > 0$ , we can choose a $C > 0$ such that $||f - g||_p \leq \epsilon/3$ with

g(x) = \begin{cases} C & f(x) > C \\ f(x) & -C \leq f(x) \leq C \\ -C & f(x) < -C \end{cases}

i.e. $g$ is $f$ bounded above and below by $C$ and $−C$ . By the Birkhoff Ergodic Theorem, $n^{-1}S_n(g)\to \bar{g}~$ $\mu$ -a.e.

Next, we note that $|n^{−1}S_n(g)| \leq C$ for all $n$ , and thus by (Dominated Convergence Theorem)[#dominated-convergence-theorem], there exists an $N$ such that for all $n > N$ ,

||n^{-1}S_n(g) - \bar{g}||_p \leq \frac{\epsilon}{3}

Applying Fatou’s Lemma gives that

||\bar{f} - \bar{g}||_p^p = \int \liminf |n^{-1}S_n(f - g)|^p\mathrm{d}\mu \leq \liminf_{n\rightarrow\infty}\int |n^{-1}S_n(f - g)|^p\mathrm{d}\mu = ||f - g||^p_p

Thus, for $n > N$ ,

||n^{-1}S_n(f) - \bar{f}||_p \leq ||n^{-1}S_n(f - g)||_p + ||n^{-1}S_n(g) - \bar{g}||_p + ||\bar{g} - \bar{f}||_p <\epsilon

Since $n^{-1}S_n(f) \overset{L^p}{\longrightarrow} \bar{f}$ , the convergence must hold in $L^1$ as well. Thus, we have

\int \bar{f}\mathrm{d}\mu = \int \lim_{n\to\infty}n^{-1}S_n(f)\mathrm{d}\mu = \lim_{n\to\infty}\int n^{-1}S_n(f)\mathrm{d}\mu = \int f\mathrm{d}\mu \\

which gives the desired result. $\square$

Law of Large Numbers, Again#

Let (Ω, F, P) be a probability space with i.i.d. real-valued random variables $\{X_i\}_{i=1}^\infty$ with distribution function $\mathrm{d}F$ . We define a map $\pi : \Omega \to S \vcentcolon= \mathbb{R}^\mathbb{N}$ by

\pi(\omega) = (X_1(\omega), X_2(\omega), \ldots)

Let $\nu=\mu\circ\pi^{-1}$ be the corresponding probability measure on $S$ .

Because the variables $\{X_i\}$ are independent, $\nu$ has the form $\nu = \mu_1\times\mu_2\times\cdots$ , and because they are identically distributed, all the marginal distributions $\mu_j$ are the same, so in fact $\nu = \mu^\mathbb{N}$ for some probability distribution $\mu$ on $\mathbb{R}$ .

For a sequence $(x_1, x_2, \ldots) \in S$ , we can define the shift map $T : S\to S$ to be

T(x_1, x_2, x_3, \ldots) = (x_2, x_3, x_4, \ldots)

Then the shift map is measure preserving and ergodic by Kolmogorov’s zero-one law.

Strong Law of Large Numbers, Again
Let $\{X_i\}_{i=1}^\infty$ be i.i.d. random variables from $\Omega$ to $\mathbb{R}$ . If $E[|X_i|] < \infty$ , then $\frac{S_n}{n} \overset{a.s.}{\longrightarrow} c$ for $c = E[X_i]$ .

Proof

Let $f : S \to \mathbb{R}$ by taking the first coordinate, that is, for $x = (x_1, x_2, \ldots)\in S$ , $f(x) = x_1$ . Then, for $T$ being the shift map and $x = \pi(\omega)$ , we have

S_n(f)(x) = f(x) + (f\circ T)(x) + \cdots + (f\circ T^{n-1}) = X_1(\omega) + X_2(\omega) + \cdots + X_n(\omega)

Thus, von Neumann’s Ergodic Theorem says that there exists an invariant $\bar{f}\in L^1$ such that

n^{-1}S_n(f)(x)\overset{a.s.}{\longrightarrow} \bar{f}

for $x\in S$ and

\int \bar{f}\mathrm{d}\mu = \int f\mathrm{d}\mu

Since $T$ is ergodic, the result from the beginning of this section states that $\bar{f} = c$ , a constant, almost surely. Thus,

c = \int \bar{f}\mathrm{d}\mu = \lim_{n\to \infty}\int n^{-1}S_n(f) = \int f\mathrm{d}\mu = E[X_i]

gives the disred result. $\square$

Measure Theory#

Measures and σ\sigmaσ-Fields#

σ\sigmaσ-Field #

Measure#

Power Set#

Semi-Ring of Sets#

Ring of Sets#

Field#

Set Function#

Outter Measure#

Caratheodory Extension Theorem#

π\piπ-System and λ\lambdaλ-System #

Dynkin π\piπ-λ\lambdaλ Theorem #

Uniquessness of Extension Thereom#

Borel σ\sigmaσ-Field#

Lebesgue Measure#

Product Measure#

Independence#

Functions, Random Variables and Integration#

Simple Functions and Random Variables#

Measurable Functions and Random Variables#

Cool facts about Measurable Functions#

Integration#

Monotone Convergence Theorem#

Fatou’s Lemma #

Dominated Convergence Theorem#

Lebesgue-Stieltjes Measure#

Radon Measure#

Product Measure#

Monotone Class#

Existence and Uniqueness of Product Measure#

Fubini-Toneli#

Probability Theory#

LpL^pLp Spaces#

Markov / Chebyshev and Jensen’s Inequalities#

Hölder and Minkowski’s Inequalities#

Convergence in Probability & Measure#

Convergence of Measure#

Convergence of Random Variables#

Hierarchy of Convergence Types#

Borel-Cantelli Lemmas#

Law of Large Numbers#

Weak Law of Large Numbers#

Strong Law of Large Numbers#

Central Limit Theorem#

Erogodic Theorem#

Birkhoff and von Neumann’s Theorems#

Law of Large Numbers, Again#

Measures and $\sigma$ -Fields#

$\sigma$ -Field #

$\pi$ -System and $\lambda$ -System #

Dynkin $\pi$ - $\lambda$ Theorem #

Borel $\sigma$ -Field#

$L^p$ Spaces#